Consider the brute force search method:
d_best = -1; r_best = -1; len_best = 0; for (d = 1; d <= N; d++) for (r = 1; r <= N; r++) { range = min( N-d+1, N-r+1); for (len = 1; len < range; len++) { // Check if there is a tree inside the pool isSolution = true; for (i = 0; i < T; i++) if ( tree i inside pool(d, r, len) ) { isSolution = false; break; } if ( isSolution ) if ( len > len_best ) { d_best = d; r_best = r; len_best = len; } } } |
When N is large (e.g.: N = 500,000), the solution will fail (Time Limit Exceeded)
d_best = -1; r_best = -1; len_best = 0; for (d = 1; d <= 500000; d++) for (r = 1; r <= 500000; r++) { range = min( N-d+1, N-r+1); for (len = 1; len < ~500000; len++) { // Check if there is a tree inside the pool isSolution = true; for (i = 0; i < T; i++) if ( tree i inside pool(d, r, len) ) { isSolution = false; break; } // This code segment executed 500000*500000*500000 times ! if ( isSolution ) if ( len > len_best ) { d_best = d; r_best = r; len_best = len; } } } |
|
Is there a way to limit the d values that needs to be considered in this for-loop ?
d_best = -1; r_best = -1; len_best = 0; for (d = 1; d <= N; d++) for (r = 1; r <= N; r++) { range = min( N-d+1, N-r+1); for (len = 1; len < range; len++) { // Check if there is a tree inside the pool isSolution = true; for (i = 0; i < T; i++) if ( tree i inside pool(d, r, len) ) { isSolution = false; break; } if ( isSolution ) if ( len > len_best ) { d_best = d; r_best = r; len_best = len; } } } |
Consider the following situation:
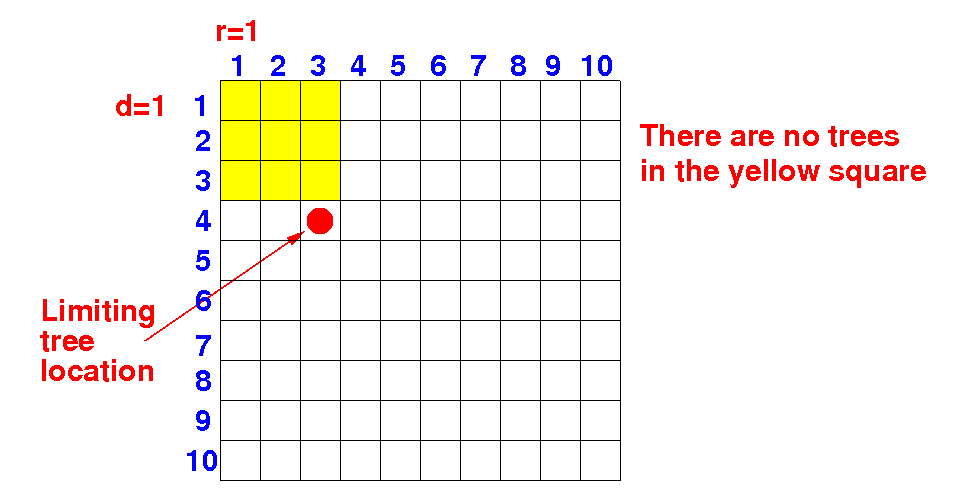
Can there be a better solution using d=2 (and r=1) ?
Can there be a better solution using d=3 (and r=1) ?
Can there be a better solution using d=4 (and r=1) ?
Can there be a better solution using d=5 (and r=1) ?
|
Consider the following situation:
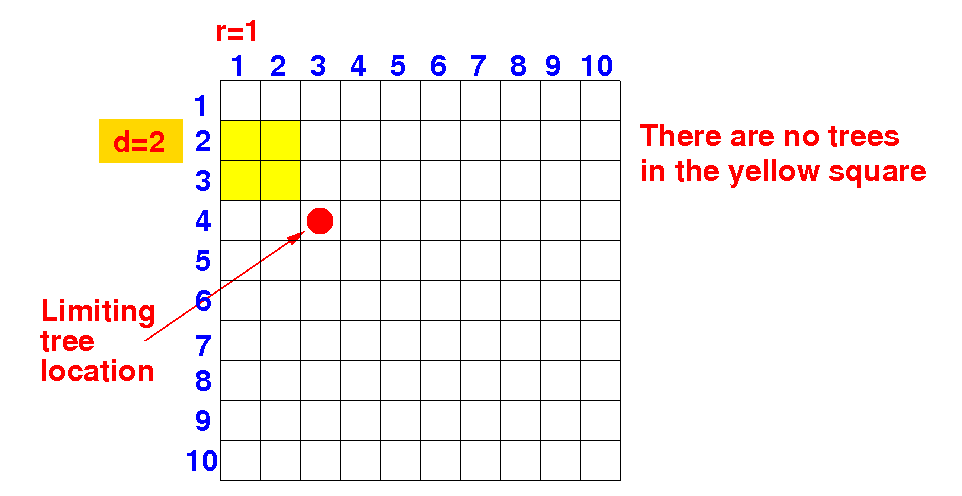
Can there be a better solution using d=2 (and r=1) ? No Can there be a better solution using d=3 (and r=1) ? Can there be a better solution using d=4 (and r=1) ? Can there be a better solution using d=5 (and r=1) ? |
Consider the following situation:
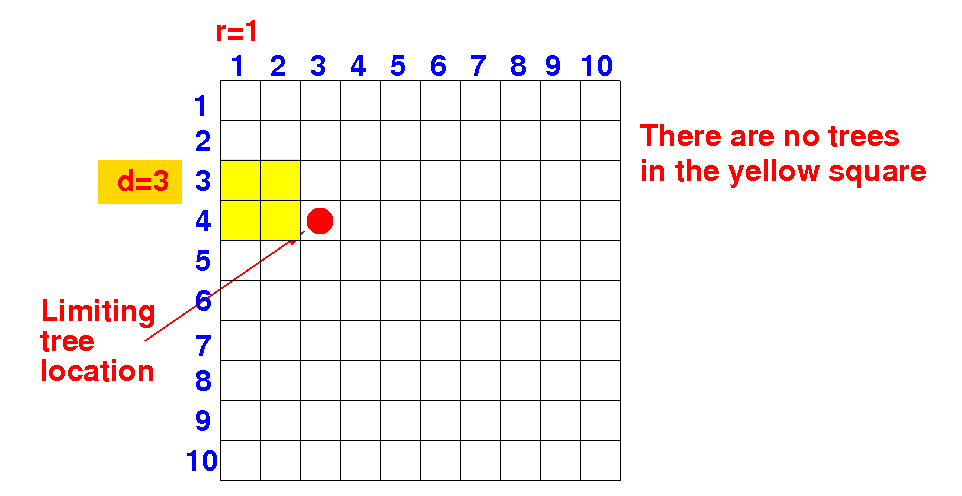
Can there be a better solution using d=2 (and r=1) ? No Can there be a better solution using d=3 (and r=1) ? No Can there be a better solution using d=4 (and r=1) ? Can there be a better solution using d=5 (and r=1) ? |
Consider the following situation:
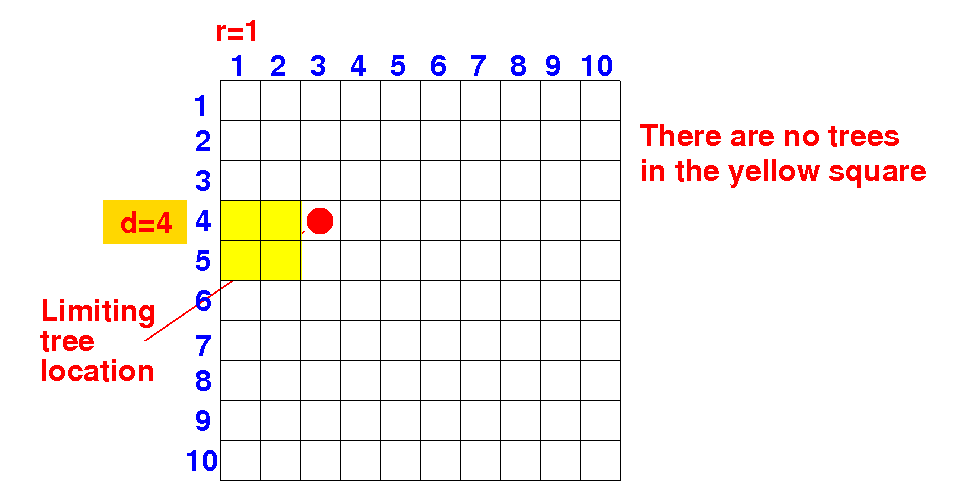
Can there be a better solution using d=2 (and r=1) ? No Can there be a better solution using d=3 (and r=1) ? No Can there be a better solution using d=4 (and r=1) ? No Can there be a better solution using d=5 (and r=1) ? |
A better solution may be found after the obstacle:
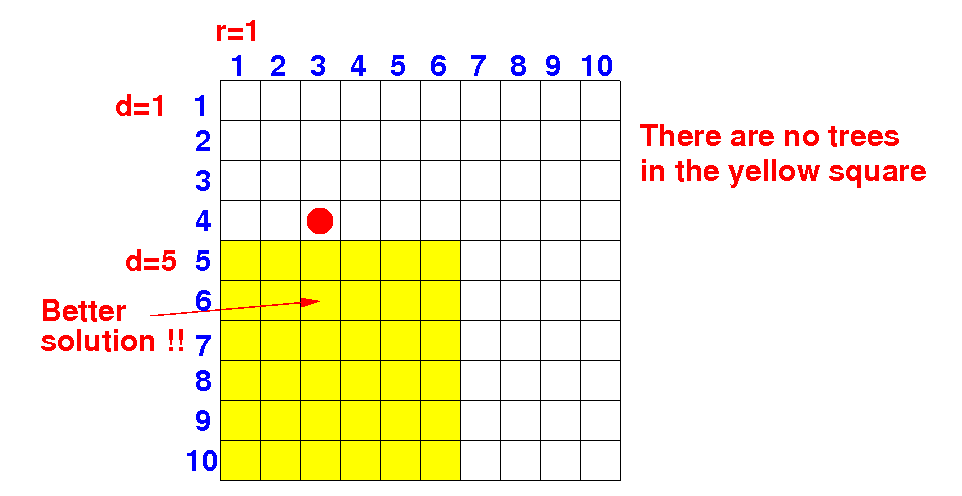
Can there be a better solution using d=2 (and r=1) ? No
Can there be a better solution using d=3 (and r=1) ? No
Can there be a better solution using d=4 (and r=1) ? No
Can there be a better solution using d=5 (and r=1) ? Yes
|
Is there a way to limit the r values that needs to be considered in this for-loop ?
d_best = -1; r_best = -1; len_best = 0; for (d = 1; d <= N; d++) for (r = 1; r <= N; r++) { range = min( N-d+1, N-r+1); for (len = 1; len < range; len++) { // Check if there is a tree inside the pool isSolution = true; for (i = 0; i < T; i++) if ( tree i inside pool(d, r, len) ) { isSolution = false; break; } if ( isSolution ) if ( len > len_best ) { d_best = d; r_best = r; len_best = len; } } } |
Consider the following situation:

Can there be a better solution using r=2 (and d=1) ? Can there be a better solution using r=3 (and d=1) ? Can there be a better solution using r=4 (and d=1) ? |
A better solution may be found after the obstacle:
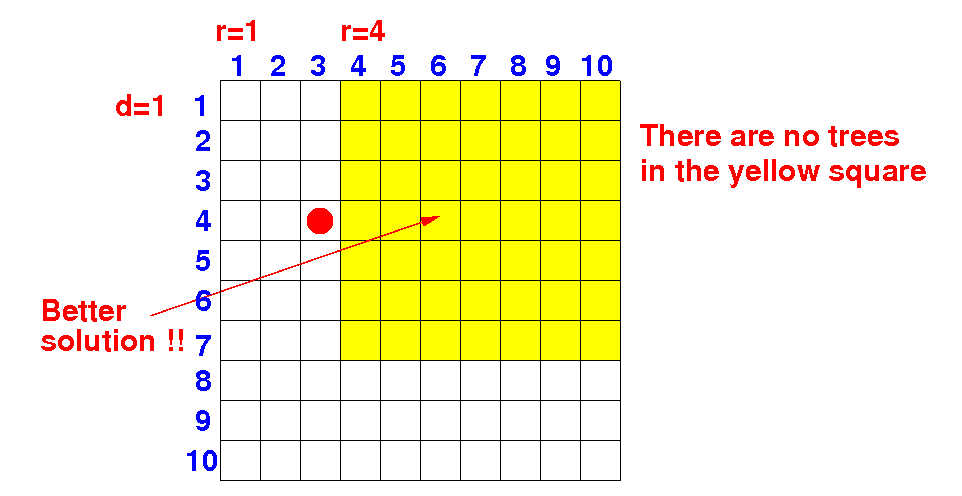
Can there be a better solution using r=2 (and d=1) ? No
Can there be a better solution using r=3 (and d=1) ? No
Can there be a better solution using r=4 (and d=1) ? Yes
|
Hypothesis derived from the previous observations:
|
Note: always verify your hypothesis with some examples !!
Consider the following input:
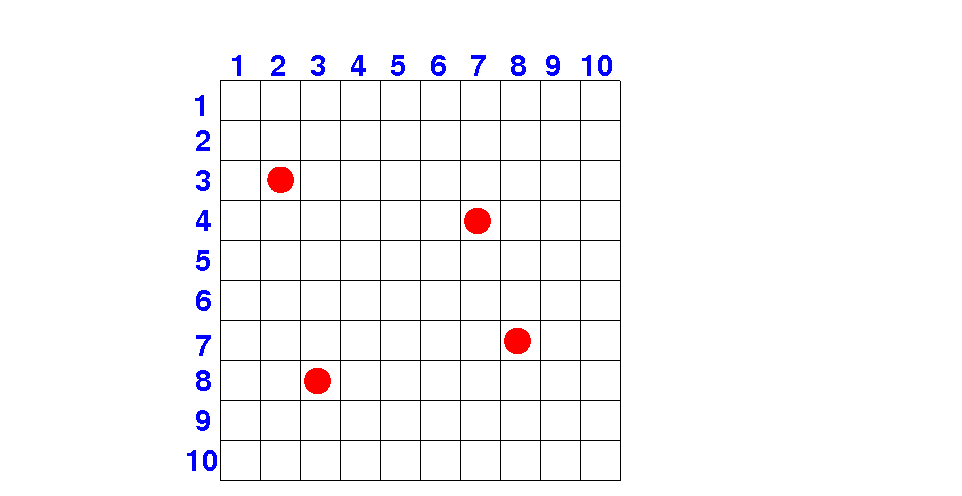
There are many pools with max length = 4...
The hypothesis states:
there is a best pool that borders on 1 or a tree !
|
Here is a maximum size pool that borders on 2 different trees:
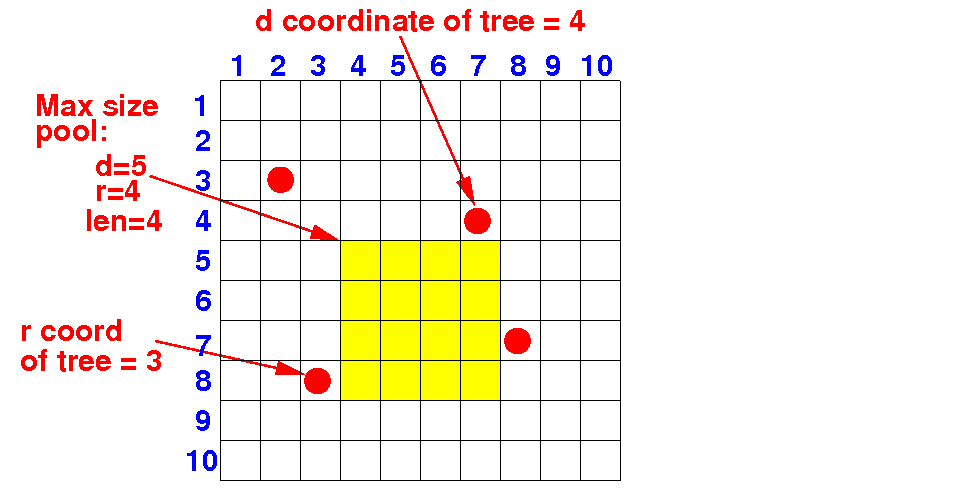
There are many pools with max length = 4...
The hypothesis states:
there is a best pool that borders on 1 or a tree !
|
Consider the example 2 from the contest:
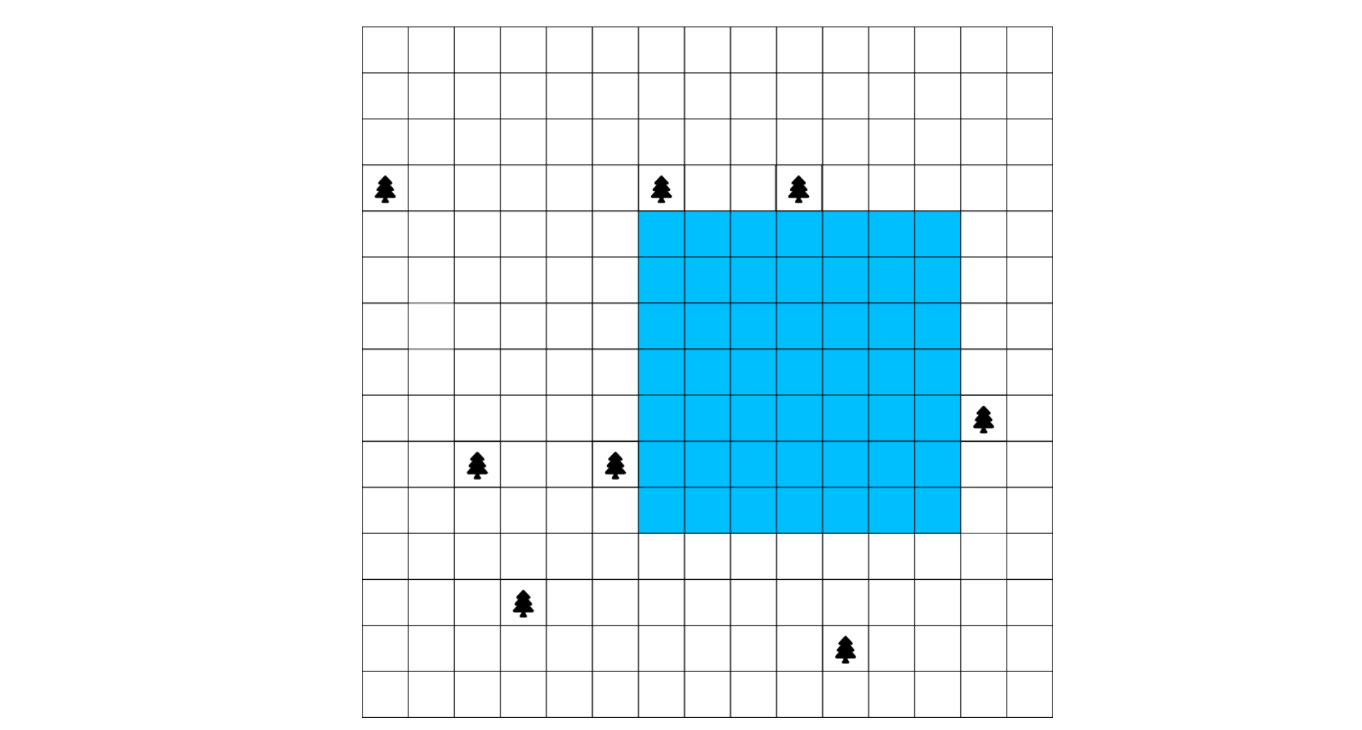
There are many pools with max length = 7...
The hypothesis states:
there is a best pool that borders on 1 or a tree !
|
Here is a maximum size pool that borders on 2 different trees:
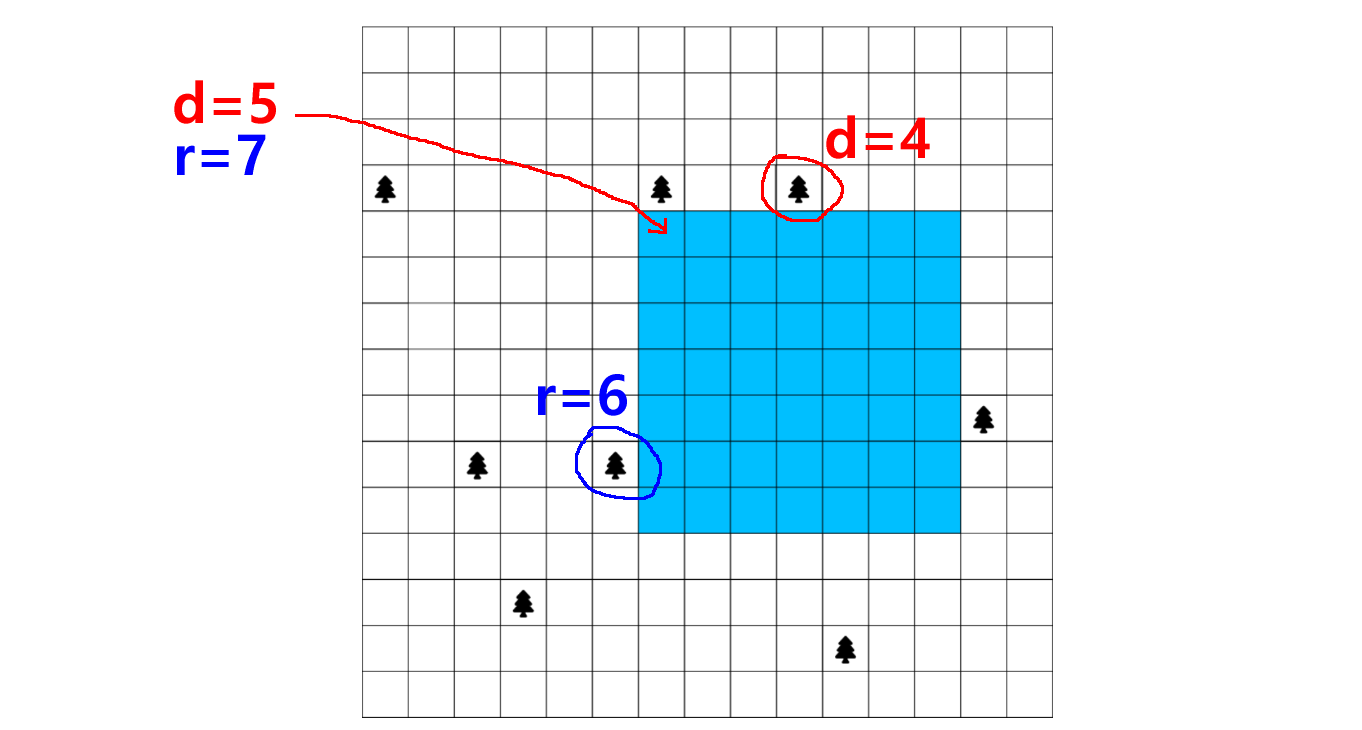
There are many pools with max length = 7...
The hypothesis states:
there is a best pool that borders on 1 or a tree !
|
Consider the original brute force search method:
d_best = -1; r_best = -1; len_best = 0; for (d = 1; d <= N; d++) for (r = 1; r <= N; r++) { range = min( N-d+1, N-r+1); for (len = 1; len < range; len++) { // Check if there is a tree inside the pool isSolution = true; for (i = 0; i < T; i++) if ( tree i inside pool(d, r, len) ) { isSolution = false; break; } if ( isSolution ) if ( len > len_best ) { d_best = d; r_best = r; len_best = len; } } } |
We can limit the d coordinates to 1 and tree[..][0]+1:
d_best = -1; r_best = -1; len_best = 0; for (d = 1, tree[0][0]+1, tree[1][0]+1, ...) for (r = 1; r <= N; r++) { range = min( N-d+1, N-r+1); for (len = 1; len < range; len++) { // Check if there is a tree inside the pool isSolution = true; for (i = 0; i < T; i++) if ( tree i inside pool(d, r, len) ) { isSolution = false; break; } if ( isSolution ) if ( len > len_best ) { d_best = d; r_best = r; len_best = len; } } } |
We can limit the r coordinates to 1 and tree[..][1]+1:
d_best = -1; r_best = -1; len_best = 0; for (d = 1, tree[0][0]+1, tree[1][0]+1, ...) for (r = 1, tree[0][1]+1, tree[1][1]+1, ...) { range = min( N-d+1, N-r+1); for (len = 1; len < range; len++) { // Check if there is a tree inside the pool isSolution = true; for (i = 0; i < T; i++) if ( tree i inside pool(d, r, len) ) { isSolution = false; break; } if ( isSolution ) if ( len > len_best ) { d_best = d; r_best = r; len_best = len; } } } |
Notice we have a extra input value 1 that needs to be considered:
d_best = -1; r_best = -1; len_best = 0; for (d = 1, tree[0][0]+1, tree[1][0]+1, ...) for (r = 1, tree[0][1]+1, tree[1][1]+1, ...) { range = min( N-d+1, N-r+1); for (len = 1; len < range; len++) { // Check if there is a tree inside the pool isSolution = true; for (i = 0; i < T; i++) if ( tree i inside pool(d, r, len) ) { isSolution = false; break; } if ( isSolution ) if ( len > len_best ) { d_best = d; r_best = r; len_best = len; } } } |
We can store this extra value in the data representation:
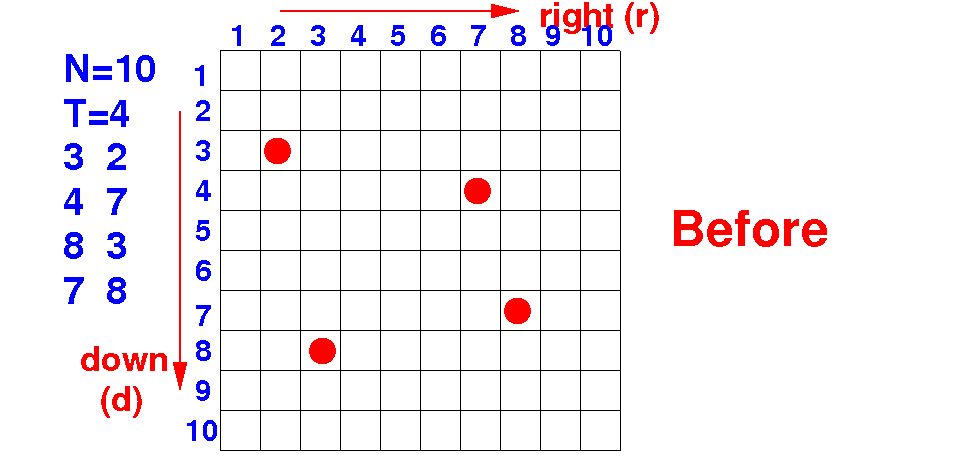
N = 10 // Grid size T = 4 // # Trees tree[0][0] = 3 tree[1][0] = 4 tree[2][0] = 8 tree[3][0] = 7 tree[0][1] = 2 tree[1][1] = 7 tree[1][1] = 3 tree[3][1] = 8 |
We can store this extra value in the data representation:
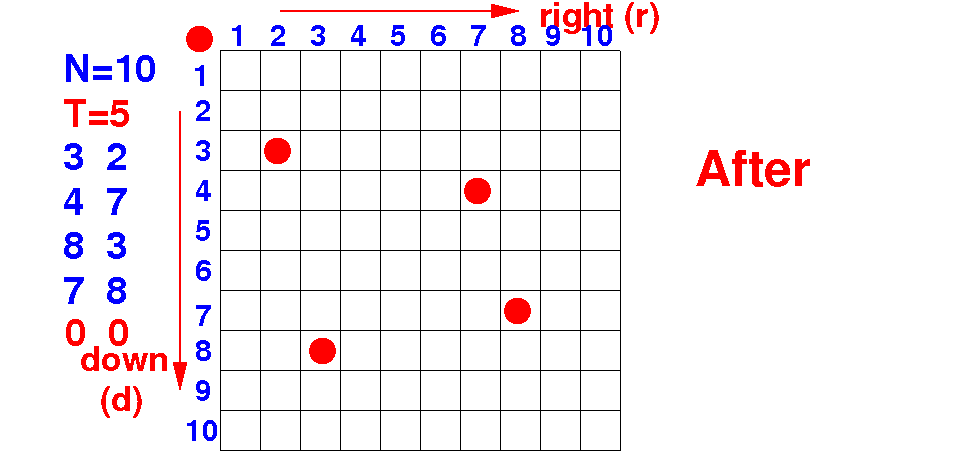
N = 10 // Grid size T = 5 // # Trees tree[0][0] = 0 tree[1][0] = 3 tree[2][0] = 4 tree[3][0] = 8 tree[4][0] = 7 tree[0][1] = 0 tree[1][1] = 2 tree[2][1] = 7 tree[3][1] = 3 tree[4][1] = 8 |
d_best = -1; r_best = -1; len_best = 0;
for (int i = 0; i < T; i++)
{ d = tree[i][0]+1;
for (int j = 0; j < T; j++)
{ r = tree[j][1]+1;
range = min( N-d+1, N-r+1);
for (len = 1; len < range; len++)
{ // Check if there is a tree inside the pool
isSolution = true;
for (i = 0; i < T; i++)
if ( tree i inside pool(d, r, len) )
{
isSolution = false;
break;
}
if ( isSolution )
if ( len > len_best )
{
d_best = d; r_best = r; len_best = len;
}
}
}
}
|
Consider the for-loop with the index len:
d_best = -1; r_best = -1; len_best = 0;
for (int i = 0; i < T; i++)
{ d = tree[i][0]+1;
for (int j = 0; j < T; j++)
{ r = tree[j][1]+1;
range = min( N-d+1, N-r+1);
for (len = 1; len < range; len++)
{ // Check if there is a tree inside the pool at (d,r)
isSolution = true;
for (i = 0; i < T; i++)
if ( tree i inside pool(d, r, len) )
{
isSolution = false;
break;
}
if ( isSolution )
if ( len > len_best )
{
d_best = d; r_best = r; len_best = len;
}
}
}
}
|
If there is a tree in the square of length len, that same tree will also be in the square of length > len
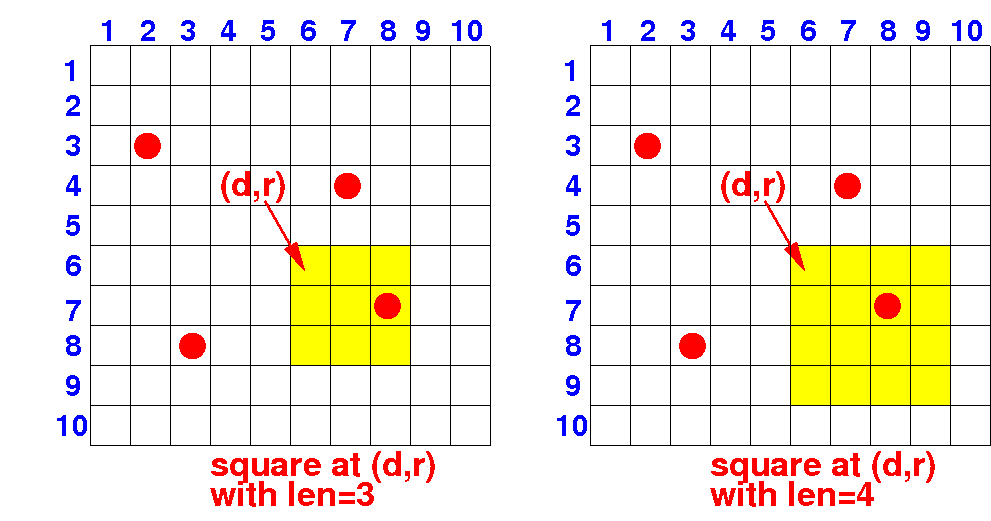
Therefore: we can abort the search for larger len values !
d_best = -1; r_best = -1; len_best = 0;
for (int i = 0; i < T; i++)
{ d = tree[i][0]+1;
for (int j = 0; j < T; j++)
{ r = tree[j][1]+1;
range = min( N-d+1, N-r+1);
for (len = 1; len < range; len++)
{ // Check if there is a tree inside the pool at (d,r)
isSolution = true;
for (i = 0; i < T; i++)
if ( tree i inside pool(d, r, len) )
{
isSolution = false;
break;
}
if ( isSolution )
if ( len > len_best )
{
d_best = d; r_best = r; len_best = len;
}
}
}
}
|
d_best = -1; r_best = -1; len_best = 0;
for (int i = 0; i < T; i++)
{ d = tree[i][0]+1;
for (int j = 0; j < T; j++)
{ r = tree[j][1]+1;
range = min( N-d+1, N-r+1);
for (len = 1; len < range; len++)
{ // Check if there is a tree inside the pool at (d,r)
isSolution = true;
for (i = 0; i < T; i++)
if ( tree i inside pool(d, r, len) )
{
isSolution = false;
break;
}
if ( !isSolution ) break; // Abort search
if ( isSolution )
if ( len > len_best )
{
d_best = d; r_best = r; len_best = len;
}
}
}
}
|
Demo: CCC/2022/Progs/j5-reduce.cc