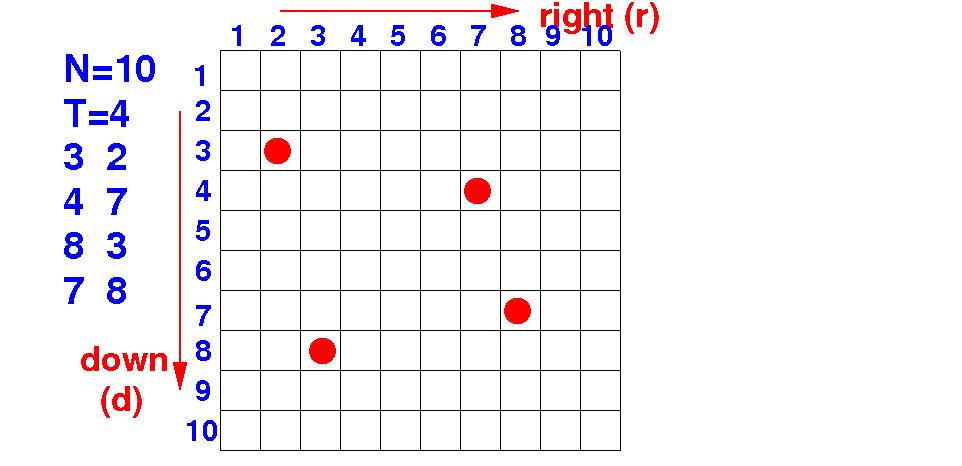
My own example to explain the solution

Consider the following input: 

 First thing you must take care of is:

    How do I store the input data ?

My own example to explain the solution

Let's use variables and arrays: 

  N = 10   // Grid size
  T = 4    // # Trees
  tree[0][0] = 3   tree[1][0] = 4   tree[2][0] = 8   tree[3][0] = 7
  tree[0][1] = 2   tree[1][1] = 7   tree[1][1] = 3   tree[3][1] = 8

My own example to explain the solution

Developing a solution: 

 First thing you must take care of is:

    How do I represent a (correct or incorrect) solution ?

My own example to explain the solution

Question:   how do we present this (square) pool ? 

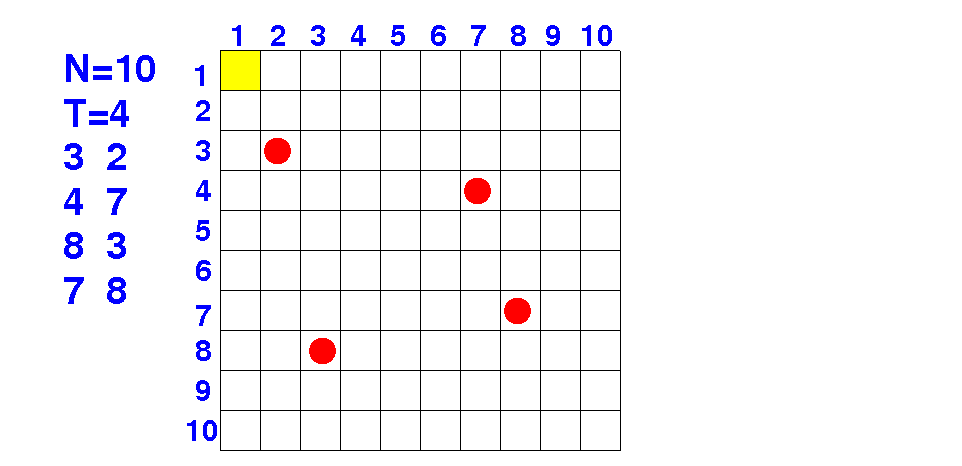
 The representation must be enable you to test for correctness !

    How do I represent the pool above ?

My own example to explain the solution

We use the upper-left corner coordinate and size and

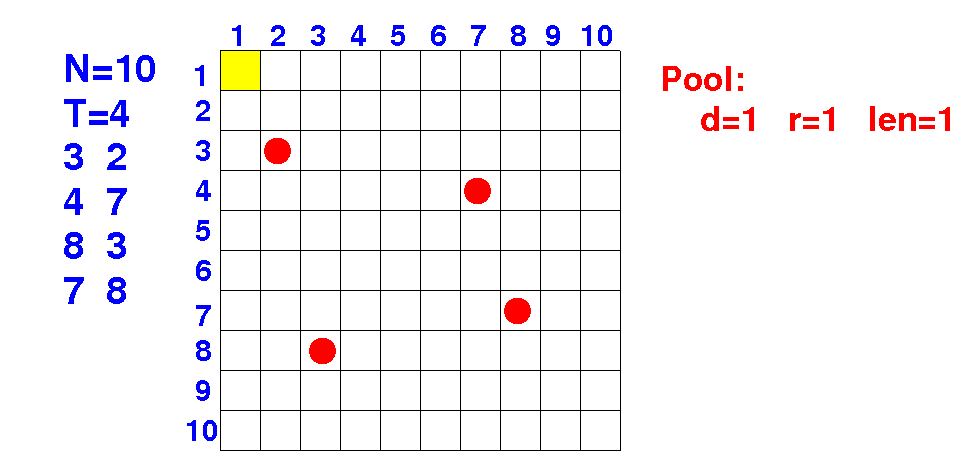
My own example to explain the solution

Quiz:   how do we present this (square) pool ?

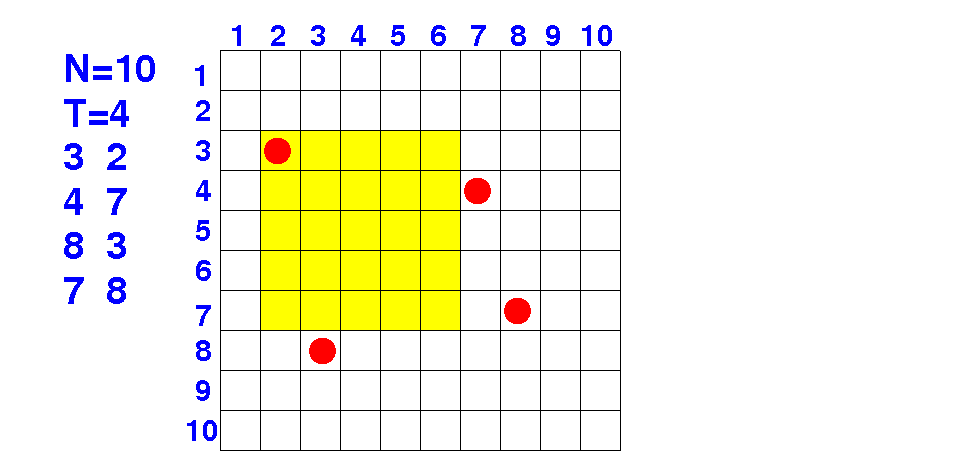
My own example to explain the solution

Answer:

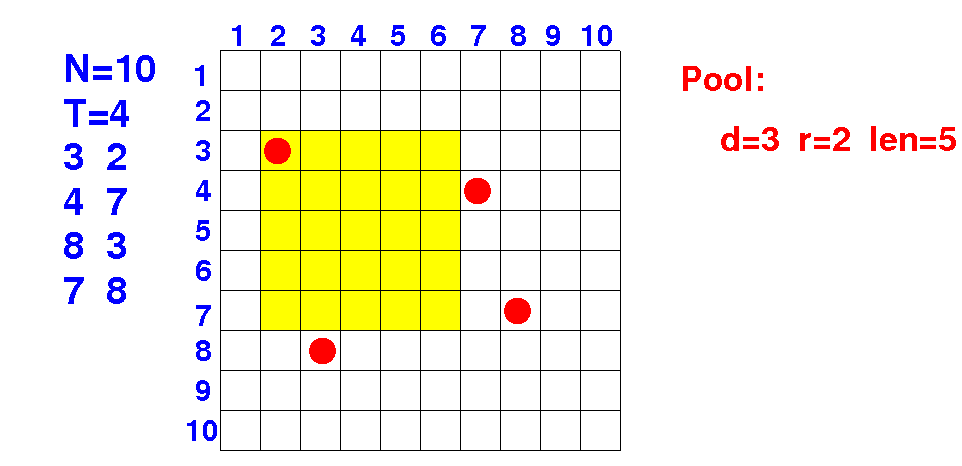
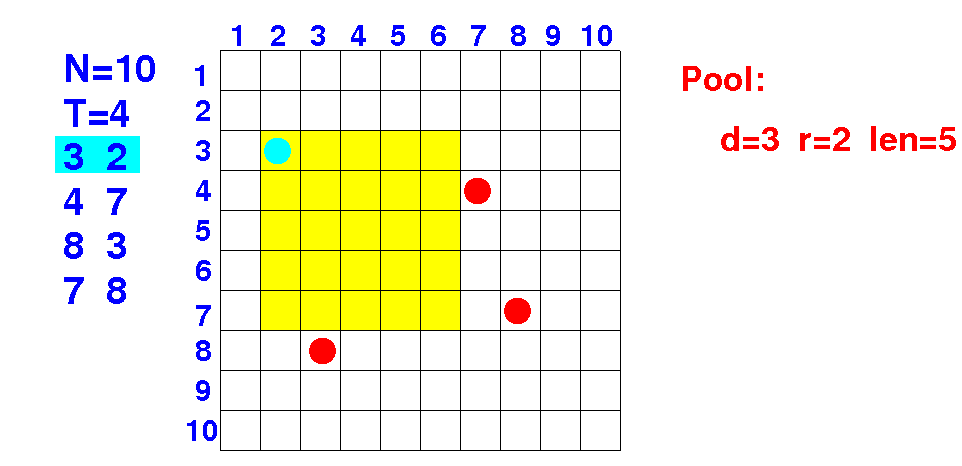
My own example to explain the solution

How can you test if the tree at coordinate 3 2 is inside the pool ???

My own example to explain the solution

The coordinates of the tree must lie within the square 

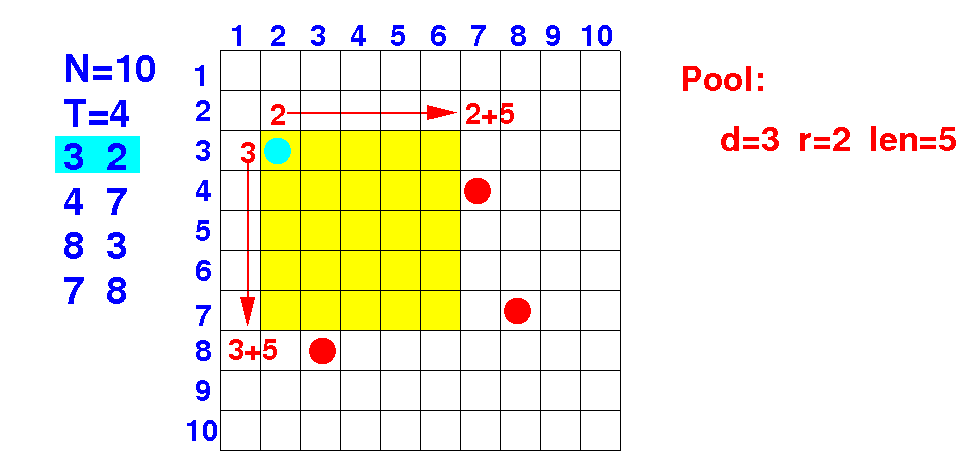
  Down  direction: 3 ≤ 3 < 3+5      ---> true
  Right direction: 2 ≤ 2 < 2+5      ---> true

My own example to explain the solution

Verify that the test can tell that the tree at coordinate 4 7 is outside the pool: 

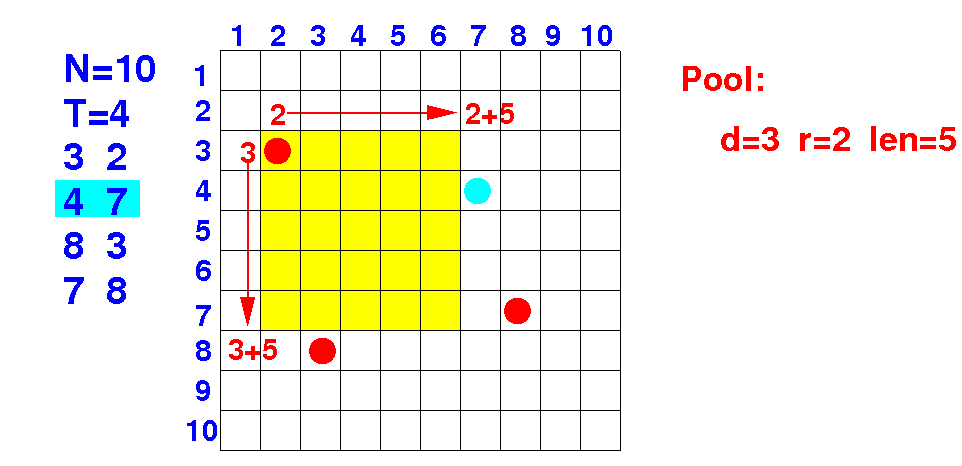
  Down  direction: 3 ≤ 4 < 3+5      ---> true
  Right direction: 2 ≤ 7 < 2+5      ---> false

The brute force search problem solving paradigm

 

  • The simplest (but inefficient) problem solving paradigm in computer science is the brute force search method

  • Brute force search method: 

      currSol = -1; // Some illegal value

  for each possible solution X
     if ( X is a correct solution )
        if ( X is better that currSol )
           currSol = X;

Use the brute force seacrh method to find a solution

Consider the following input: 

 First thing you must do to apply brute force search:

    How do I generate every possible solution ? (including incorrect ones)

Use the brute force seacrh method to find a solution

Generating every possible pool: 

  (1) Consider every possible placement of a pool

Use the brute force seacrh method to find a solution

Generating every possible pool: 

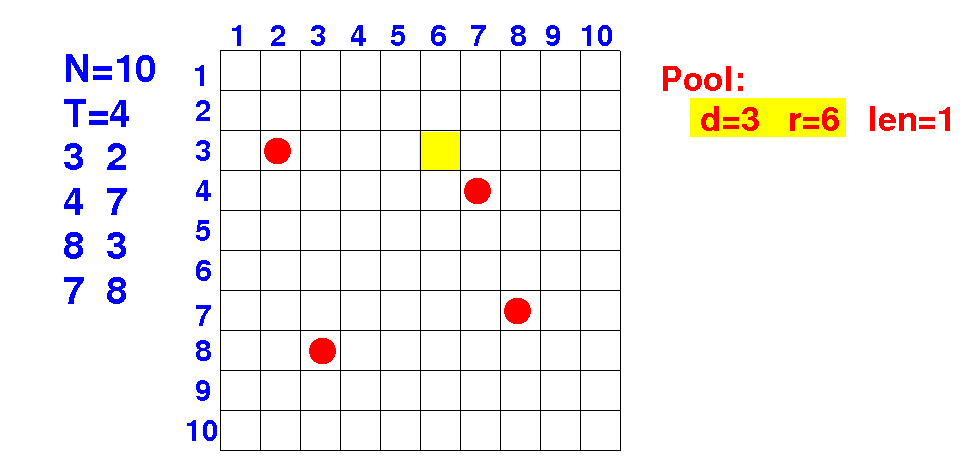
  (1) Consider every possible placement of a pool

      for (d = 1; d <= 10; d++)
         for (r = 1; r <= 10; r++)

Use the brute force seacrh method to find a solution

Generating every possible pool: 

  (1) Consider every possible placement of a pool

      (2) For each placement, try all possible sizes
         --> len = 1

Use the brute force seacrh method to find a solution

Generating every possible pool: 

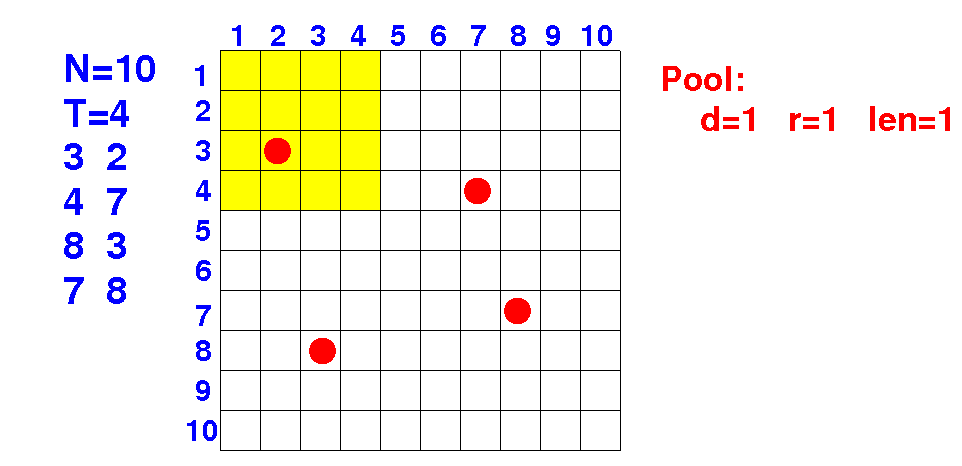
  (1) Consider every possible placement of a pool

      (2) For each placement, try all possible sizes
         --> len = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

Use the brute force seacrh method to find a solution

What are all the possible lengths for a pool placed at coordinate 5 8 ? 

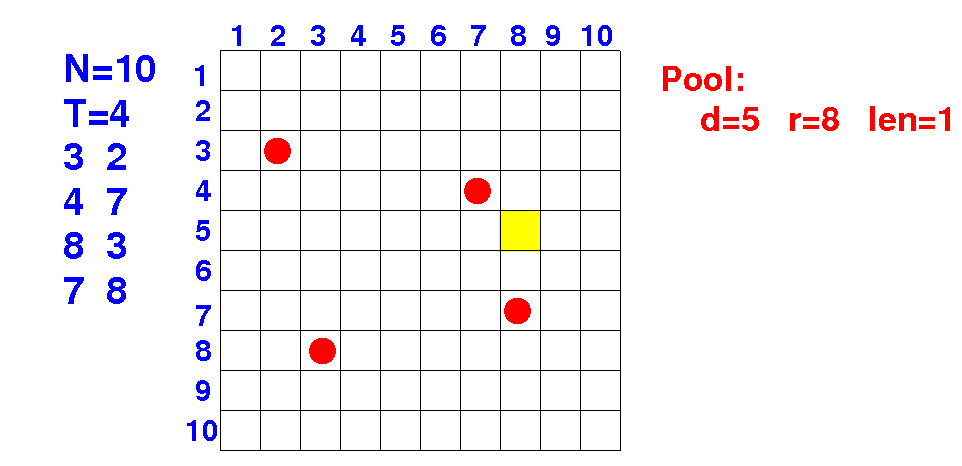
  (1) Consider every possible placement of a pool

      (2) For each placement, try all possible sizes
         --> len = 1, ... ???

Use the brute force seacrh method to find a solution

What are all the possible lengths for a pool placed at coordinate 5 8 ?   Answer: 1, 2, 3 

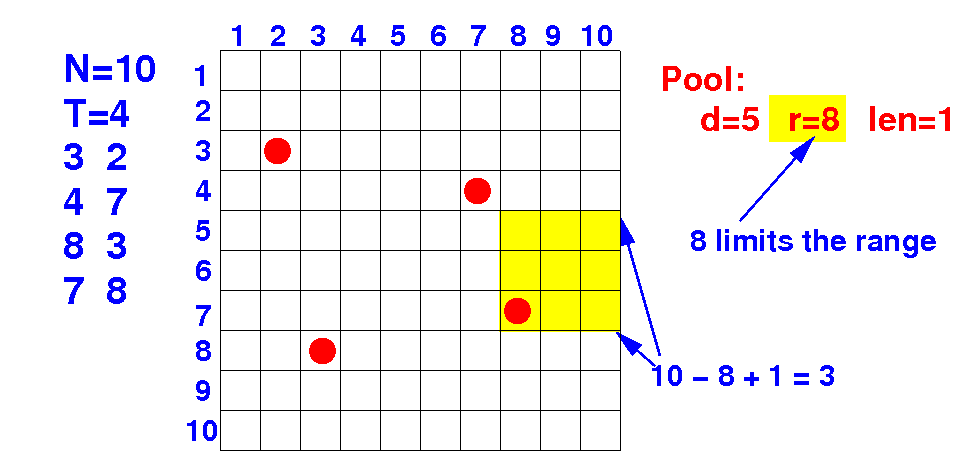
  (1) Consider every possible placement of a pool

      (2) For each placement, try all possible sizes
         --> len = 1, 2, 3

Use the brute force seacrh method to find a solution

What are all the possible lengths for a pool placed at coordinate 7 3 ? 

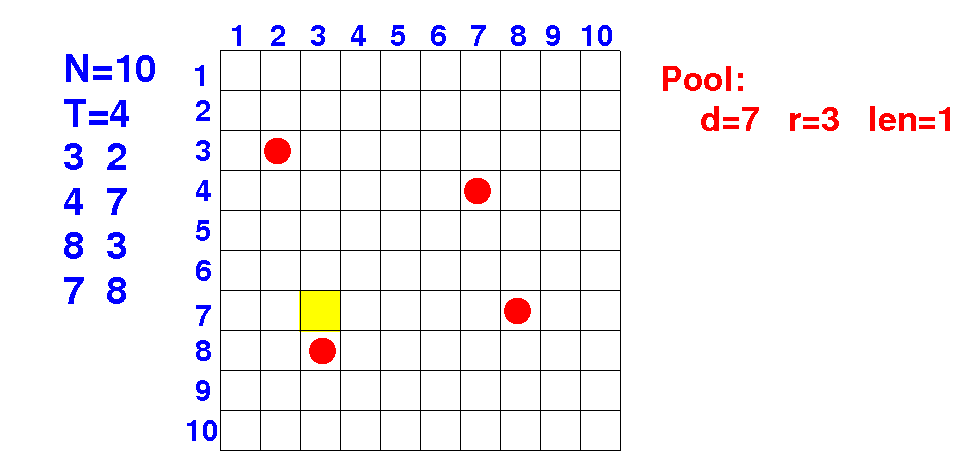
  (1) Consider every possible placement of a pool

      (2) For each placement, try all possible sizes
         --> len = 1, ... ???

Use the brute force seacrh method to find a solution

What are all the possible lengths for a pool placed at coordinate 5 8 ?   Answer: 1, 2, 3, 4 

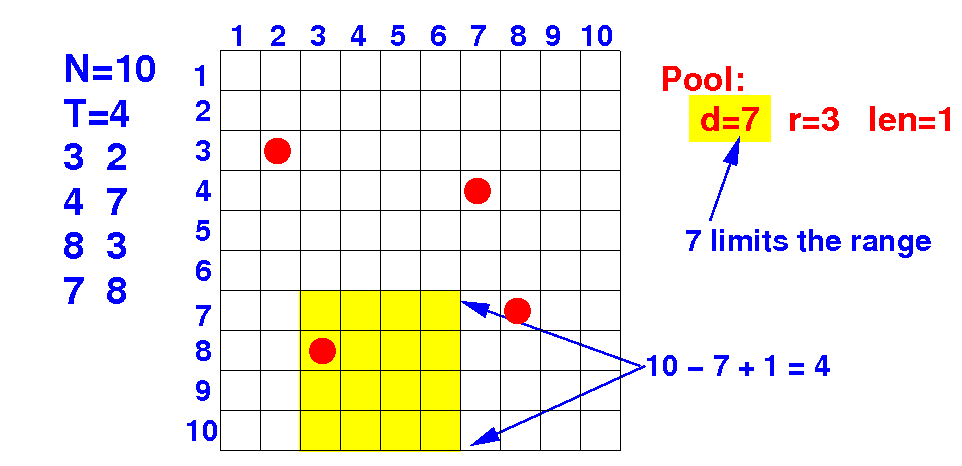
  (1) Consider every possible placement of a pool

      (2) For each placement, try all possible sizes
         --> len = 1, 2, 3, 4

Use the brute force seacrh method to find a solution

How to generate all the possible pools: 

  for (d = 1; d <= 10; d++)
     for (r = 1; r <= 10; r++)
        range = min( 10-d+1, 10-r+1);
        for (len = 1; len < range; len++)

The brute force search method to find the largest pool 

  d_best = -1; r_best = -1; len_best = 0;

  for (d = 1; d <= N; d++)
     for (r = 1; r <= N; r++)
     {
        range = min( N-d+1, N-r+1);
        for (len = 1; len < range; len++)
        {  // Check if there is a tree inside the pool

           isSolution = true;

           for (i = 0; i < T; i++) // Exercise:translate this into code  
              if ( tree i inside pool(d, r, len) ) // See notes...
              {
                 isSolution = false;
                 break;
              }

           if ( isSolution )
              if ( len > len_best )
              {
                 d_best = d; r_best = r; len_best = len;
              }
        }
     }

Demo: CCC/2022/Progs/j5.cc