Brute force solution....

 

  • This problem can easily be solved using a brute force solution...

  • However, the brute force solution will run very slowly due to the huge amount of input commands:

      • MN can be 5,000,000
      • K can be 1,000,000     

    So you may be flipping around 1,000,000,000,000 cells from one color to the other....

  • Nevertheless, let's start by writing the brute force method...

Representing the colors in a cell

 

  • Because there are 2 colors and each brush stroke flips the color in a cell, we use a boolean 2-dim array to represent the canvas: 

       // Initialize grid to all black

   bool grid[m+1][n+1];     // We will use  grid[1..m][1..n]

   for ( int x = 1; x <= m; x++ )
      for ( int y = 1; y <= n; y++ )
          grid[x][y] = false;           // false = B (true = gold)

The brute force algorithm

The brute force algorithm: 

   cin >> k;  // k = # commands of the painter   

   for ( int q = 0; q < k; q++ )
   {
      cin >> letter;
      cin >> number;

      if  ( letter == 'R' )
      {
         // Flip row "number"
         for ( int y = 1; y <= n; y++ )
            grid[number][y] = ! grid[number][y]; 
                  // Note: !true = false, !false = true 
     }
      else
      {
         // Flip column "number"
         for ( int x = 1; x <= m; x++ )
            grid[x][number] = ! grid[x][number];
                  // Note: !true = false, !false = true
      }
   }

DEMO: CCC/2021/Progs/j5-brute-force.cc

How to make an efficient solution ?

  • To find an efficient solution, we need to apply logic and mathematics

  • We need to use the mathematical concept of commutativity to re-write the input !

  • An operation ⊕ is commutative if: 

          a ⊕ b = b ⊕ a

  • Key:

      • The commutative property allows us to re-order operations

      • 2 (or more) operations may cancel each other !!!

How to show than an 2 operations are commutative

  • The operations a and b are commutative if for an arbitrary state X of the system, this holds: 

      Start in state X

      (1a) Apply this order of operations

                 a ⊕ b     // ⊕ means: "then"

      (1b) Let Z1 = state after applying a ⊕ b

  Start in state X

      (2a) Apply this order of operations

                 b ⊕ a

      (2b) Let Z2 = state after applying a ⊕ b

  We always have:   Z1 = Z2

How to show that R m and C n are commutative 

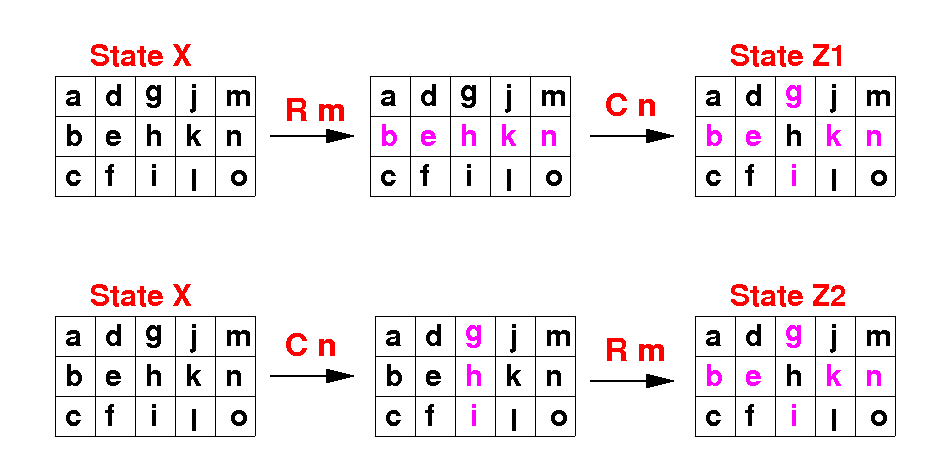
 We can start in any state of the canvas
 We apply  R m and then C n
 The result is Z1

 We start again in any state of the canvas
 We apply  C n and then R m
 The result is Z2

 We get the same result ! So order does not matter

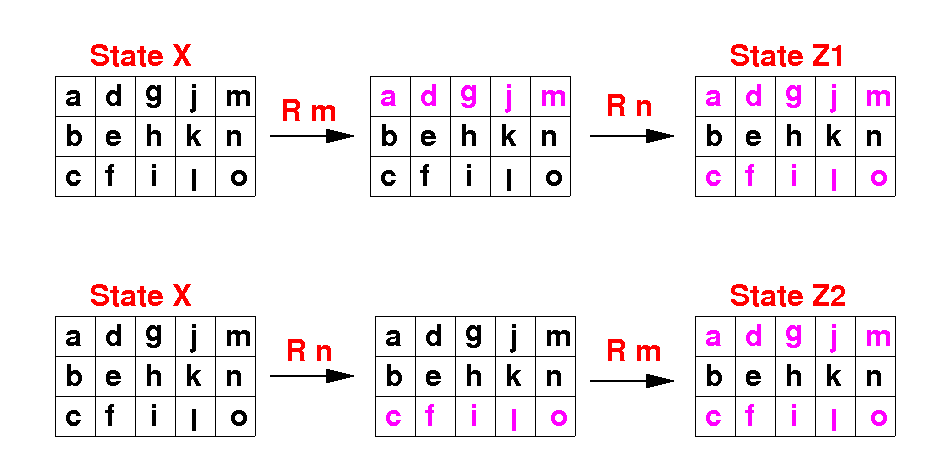
How to show that R m and R n are commutative 

 We can start in any state of the canvas
 We apply  R m and then R n
 The result is Z1

 We start again in any state of the canvas
 We apply  R n and then R m
 The result is Z2

 We get the same result ! So order does not matter

Note:   Same for C m and C n

Conclussion

 

  • All the painting operations commute

  • Therefore:

      • The order in which you apply the operations is not important

 

There is one more property that you need to discover to get a speedy algorithm.

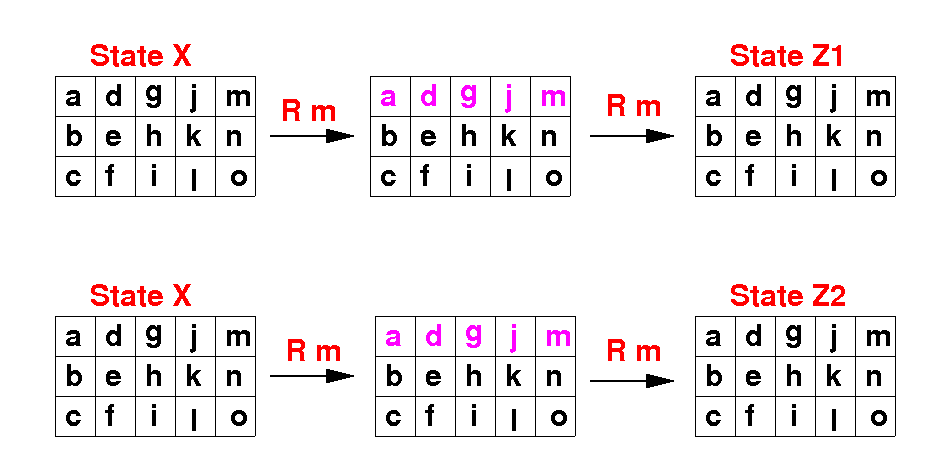
Notice that R m and R m is a NULL operation 

 R m  and  R m  not only commute
 The cancel each other out !!

 The trick to speed up the solution is:

    Cancel as many operations out as you can.

Note:   Same for C n and C n - they also cancel

Speedier algorithm

  

   cin >> k;  // k = # commands of the painter   

   /* -------------------------------------
      Store all the painting commands 
      ------------------------------------- */
   for ( int q = 0; q < k; q++ )
   {
      Read in a command;
      Store it;
   }

   /* ---------------------------------------------
      Perform ONLY commands issued ODD # times !
      --------------------------------------------- */
   for ( each command X )
   {
      if ( command X is issued an odd number of times )
         do the command
   }

Task: finds a data structure that allows you to count the different commands fast !

Fast solution to J5: pre-processing 
   // Used to eliminate duplicate commands
   int Rcommands[m+1], Ccommands[n+1];

   for (int x = 1; x <= m; x++)
       Rcommands[x] = 0;
   for (int x = 1; x <= n; x++)
       Ccommands[x] = 0;

   // Read in commands
   int k;
   cin >> k;

   char letter;
   int  number;

   // Read in commands and COLLADE duplicate commands
   for ( int q = 0; q < k; q++ )
   {
      cin >> letter;
      cin >> number;

      if ( letter == 'R' )
         Rcommands[number]++;  // One more R n
      else
         Ccommands[number]++;  // One more C n
   }

Fast solution to J5: process paint commands 
   bool grid[m+1][n+1];

   for ( int x = 1; x <= m; x++ )
      for ( int y = 1; y <= n; y++ )
          grid[x][y] = false;           // false = B

   // Process Row commands
   for ( int x = 1; x <= m; x++ )
      if ( Rcommands[x]%2 == 1 )
         // Flip row x if this R command has an ODD count
         for ( int y = 1; y <= n; y++ )
             grid[x][y] = ! grid[x][y];  // !true = false, !false = true

   // Process Column commands
   for ( int y = 1; y <= n; y++ )
      if ( Ccommands[y]%2 == 1 )
         // Flip column y if this C command has an ODD count
         for ( int x = 1; x <= m; x++ )
             grid[x][y] = ! grid[x][y];  // !true = false, !false = true

You can count the number of true values in the cells...