Finding the
minimum
number of
swaps
to arrange books
Sample input:
You can swap any book with any other book
Arrange the books in the order of:
Large Medium Small
|
Finding the
minimum
number of
swaps
to arrange books
Sample output:
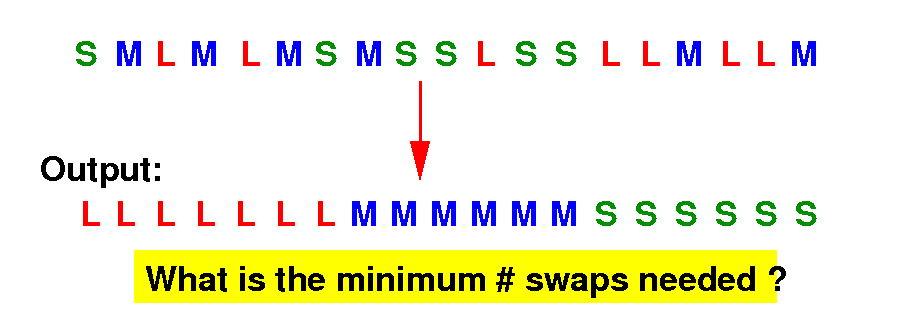
Question:
What is the minimum # swaps needed to re-arranged the books to:
Large Medium Small
|
This problem calls for
creativity....
This problem tests whether you can figure out the best way to re-arrange the books:
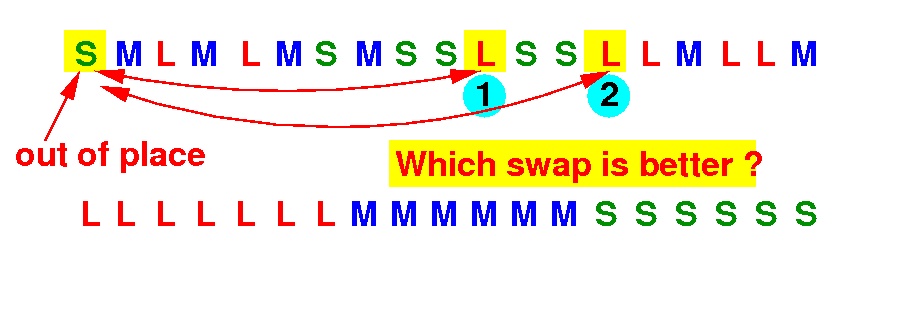
Question:
Which swap is better ?
(1) Swap the out-of-place S book with the first L book ?
(2) Swap the out-of-place S book with the second L book ?
|
This problem calls for
creativity....
Suppose we swap the out-of-place S book with the first L book:
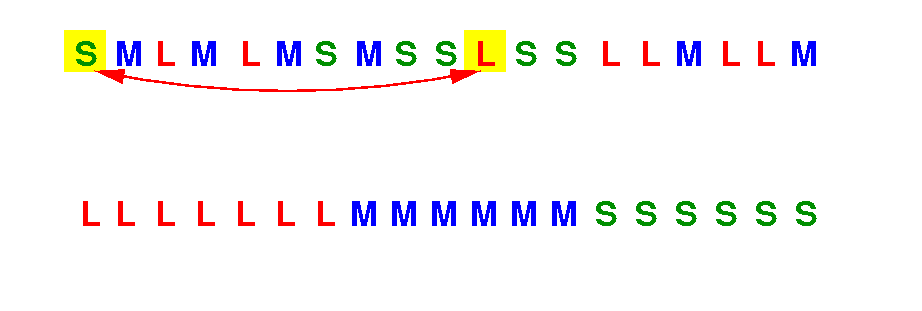
Question:
Which swap is better ?
(1) Swap the out-of-place S book with the first L book ?
(2) Swap the out-of-place S book with the second L book ?
|
This problem calls for
creativity....
This swap will only move 1 book (L) in-place. The S book is still out-of-place !
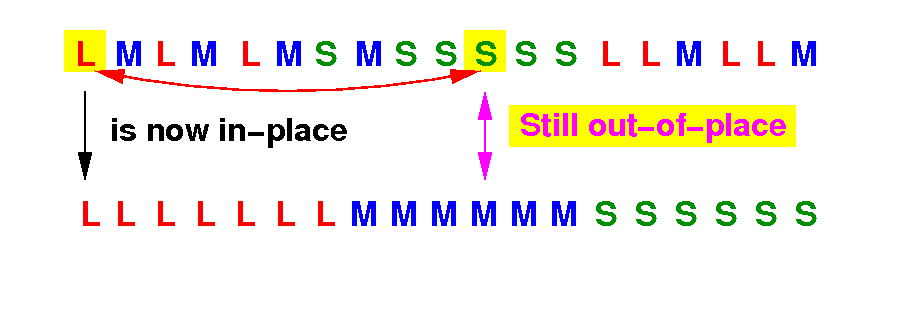
Question:
Which swap is better ?
(1) Swap the out-of-place S book with the first L book ?
(2) Swap the out-of-place S book with the second L book ?
|
This problem calls for
creativity....
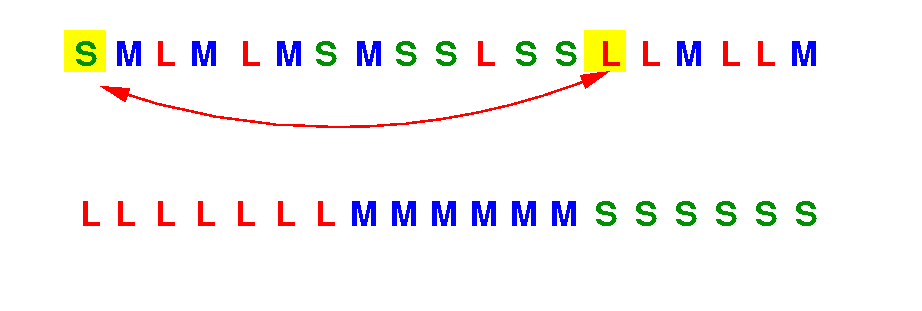
Suppose we swap the out-of-place S book with the second L book:
Question:
Which swap is better ?
(1) Swap the out-of-place S book with the first L book ?
(2) Swap the out-of-place S book with the second L book ?
|
This problem calls for
creativity....
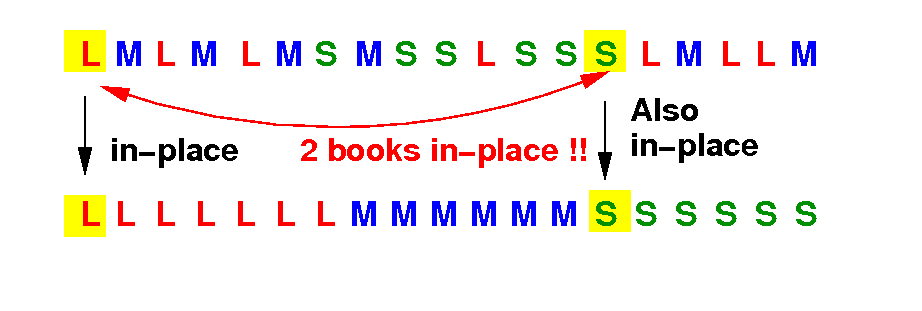
This swap will move both (= 2!!) books (L and S) in-place !!!!
Question:
Which swap is better ?
(1) Swap the out-of-place S book with the first L book ?
(2) Swap the out-of-place S book with the second L book ?
Clearly, swap (2) is better !
|
Determining the sections of
each book size
(L, M and S section)
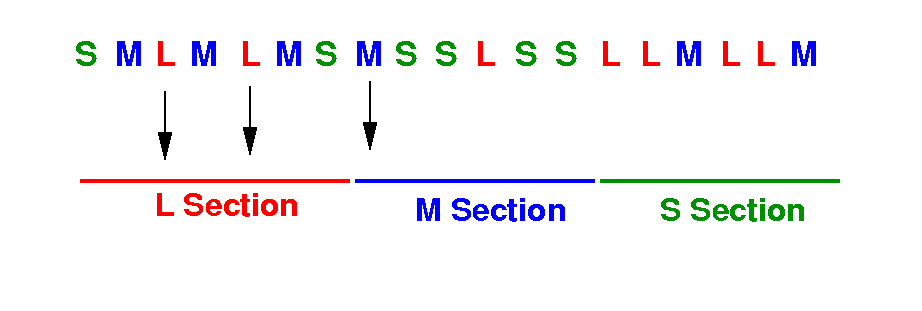
To determine if a book is in-place or out-of-place, we need to find the different book sections:
Question:
How can you determine the section for each size of books ?
|
Determining the sections of
each book size
(L, M and S section)
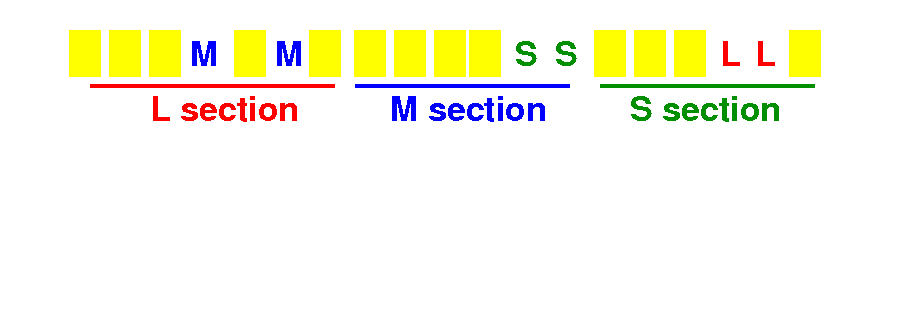
We can count the number of books of each size to determine each section size:
You can count each type books in the input
for ( int i = 0; i < letters.length(); i++ )
{
if ( letters[i] == 'L' ) LCount++;
if ( letters[i] == 'M' ) MCount++;
if ( letters[i] == 'S' ) SCount++;
}
|
Determining the sections of
each book size
(L, M and S section)
The sections of each book size can be determined as follows:
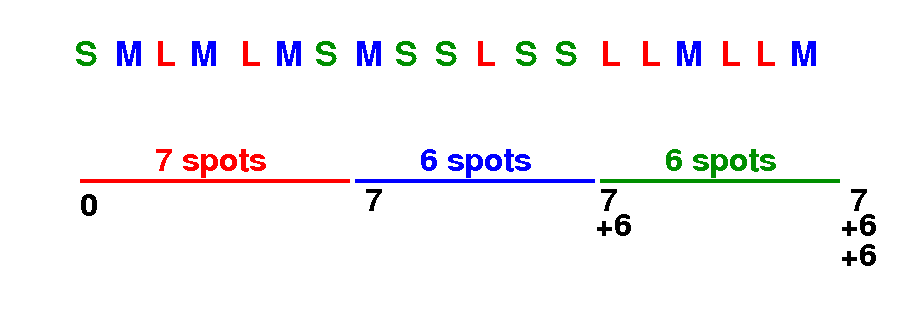
L section: 0 ≤ i < LCount M section: LCount ≤ i < LCount + MCount S section: LCount + MCount ≤ i < LCount + MCount + SCount |
Prelude:
an important observation to make things
easier to
explain
Notice that there is no need to swap the books that are already in their section:
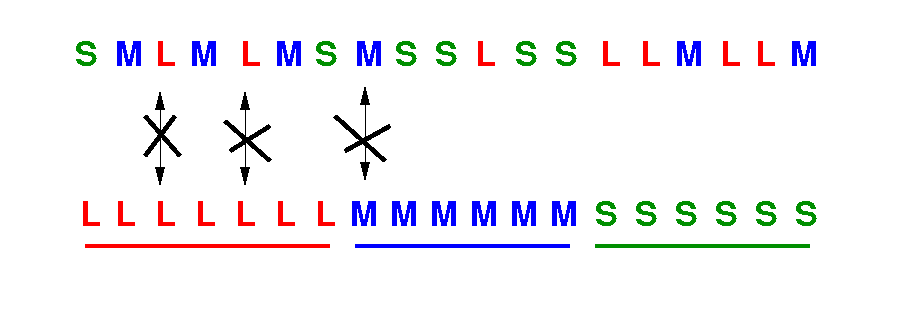
Swapping books that are already in-place cost extra swaps !! So swapping books that are already in-place will give an incorrect solution ! |
Prelude:
an important observation to make things
easier to
explain
Because there is no need to consider books that are already in their section, we can leave them out:
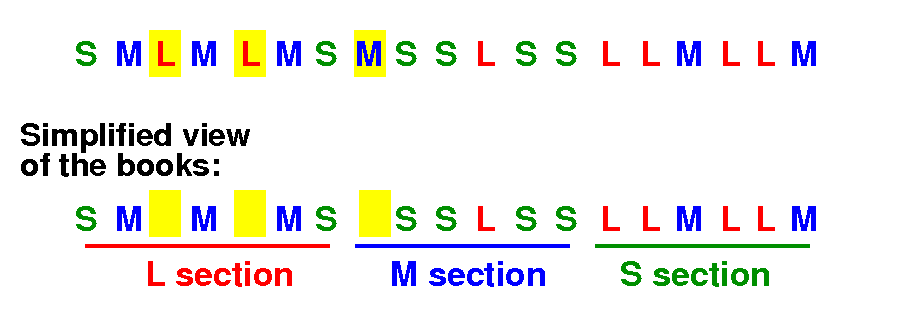
We only need to consider books that are out-of-place !
|
Step 1: determine the
best possible swaps
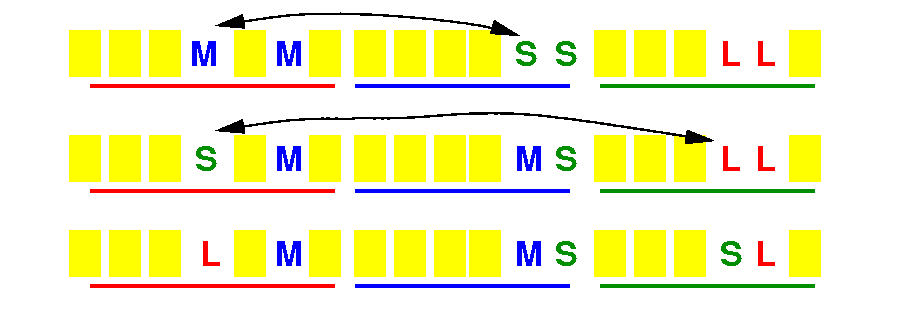
How many direct swaps can we do to between L <==> M
|
Step 1: determine the
best possible swaps
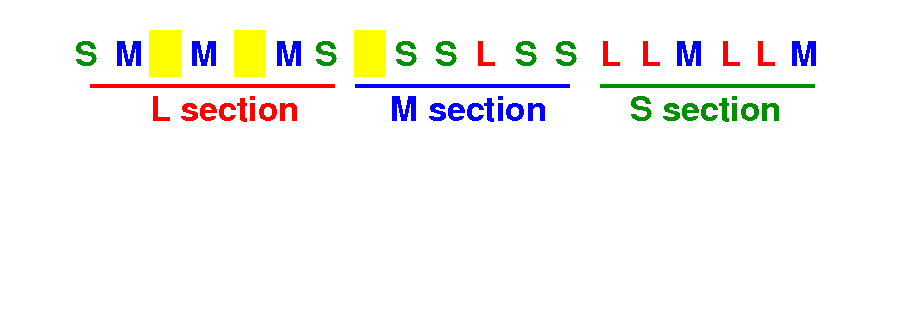
How many direct swaps can we do to between L <==> M
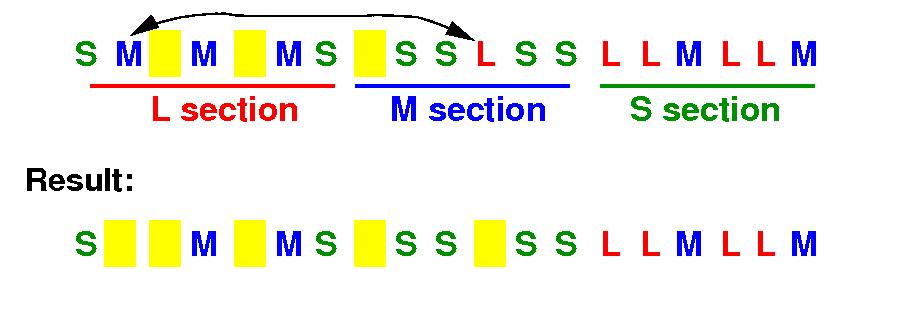
Count M's inside the L section: 3 Ms
Count L's inside the M section: 1 L
# direct swaps between L <==> M = min(3,1) = 1
# swaps = 1
|
Step 1: determine the
best possible swaps
How many direct swaps can we do to between L <==> S
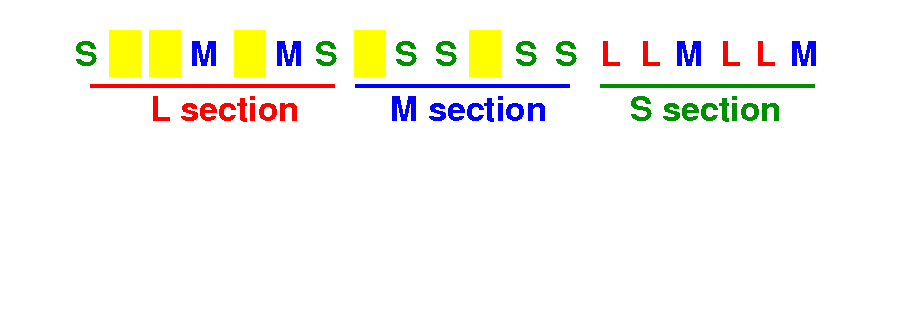
# swaps = 1
|
Step 1: determine the
best possible swaps
How many direct swaps can we do to between L <==> S
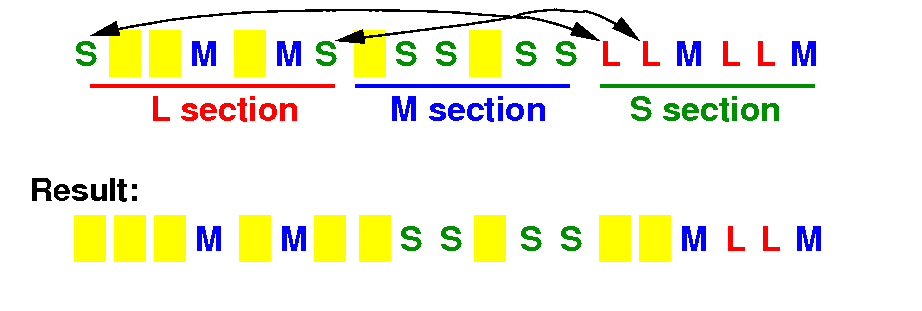
Count S's inside the L section: 2 Ss
Count L's inside the S section: 4 Ls
# direct swaps between L <==> S = min(2,4) = 2
# swaps = 1+2
|
Step 1: determine the
best possible swaps
How many direct swaps can we do to between M <==> S
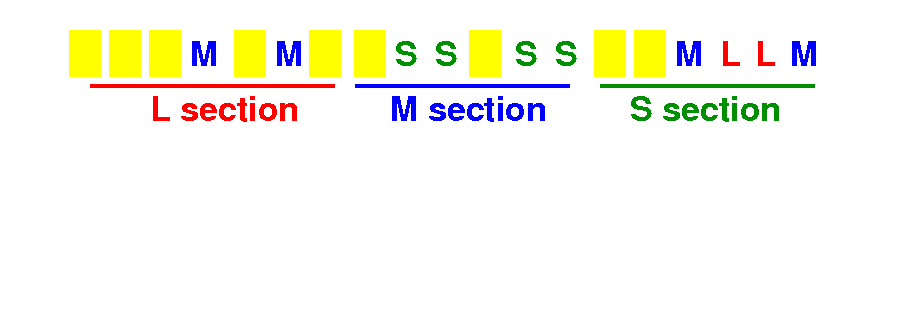
# swaps = 1+2
|
Step 1: determine the
best possible swaps
How many direct swaps can we do to between M <==> S
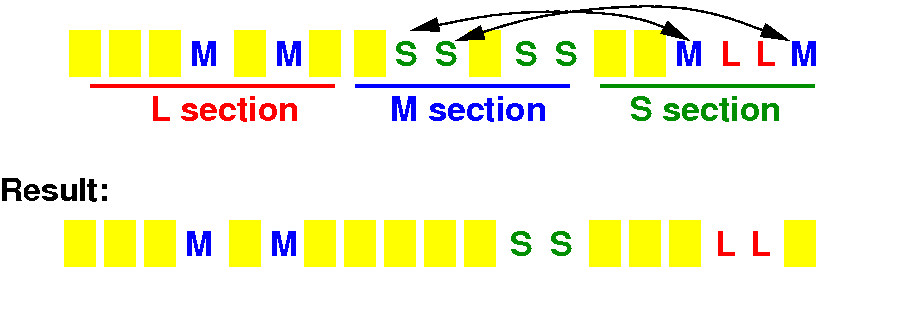
Count S's inside the M section: 4 Ss
Count M's inside the S section: 2 Ms
# direct swaps between M <==> S = min(4,2) = 2
# swaps = 1+2+2
|
Step 2: swap the
remaining books
We will always end up with triplets like this:
Case 1: (M, S, L) (= rotate (L, M, S) left)
L section contains only M books
M section contains only S books
S section contains only L books
Case 1: (S, L, M) (= rotate (L, M, S) right)
L section contains only S books
M section contains only L books
S section contains only M books
|
Step 2: swap the
remaining books
Each triplet (L, M, S) can be re-arranged in-place with 2 swaps:
Now we can write an algorithm to determine the
minumum number of swaps
|
Problem J4 solution in Pseudo Code (high level description)
letters = input string (e.g.: "LLSLM") // Find the section sizes int LCount = 0, MCount = 0, SCount = 0; // Initialize counts for ( int i = 0; i < letters.length(); i++ ) { if ( letters[i] == 'L' ) LCount++; if ( letters[i] == 'M' ) MCount++; if ( letters[i] == 'S' ) SCount++; } int swaps = 0; /* ------------------------------------------- (1) Count the direct swaps ------------------------------------------- */ int maxDirectSwaps; /* --------------------------------------- Find # out-of-place books in Section L --------------------------------------- */ int sectionL_Ms = 0, sectionL_Ss = 0; for ( int i = 0; i < LCount; i++ ) { if ( letters[i] == 'M' ) sectionL_Ms++; if ( letters[i] == 'S' ) sectionL_Ss++; } // Do the same for Sections M and S /* ---------------------------------------------- Find and count the DIRECT swaps (best) ---------------------------------------------- */ // (1) Direct swap between L <--> M maxDirectSwaps = min(sectionL_Ms, sectionM_Ls); swaps += maxDirectSwaps; // Update # swaps sectionL_Ms -= maxDirectSwaps; // Reduce # out-of-place M books in section L sectionM_Ls -= maxDirectSwaps; // Reduce # out-of-place L books in section M // Do the same for L <--> S and M <--> S /* ---------------------------------------------- Handle the triplets with 2 swaps ---------------------------------------------- */ NTriplets = (sectionL_Ms + sectionL_Ss + sectionM_Ls + sectionM_Ss + sectionS_Ls + sectionS_Ms)/3; swaps += 2*NTriplets cout << "Solution: " << swaps << endl; |
Demo: CCC/2021/Progs/j4.cc