Translating the Escape Room problem into a Graph

The Escape Room is actually a directed graph where:

Translating the Escape Room problem into a Graph

The question is basically a graph traversal problem:

Graph Traversal Algorithms

There are 2 classic graph traversal algorithms:
Both algorithms are equally fast
However:

The recursive Depth First Search algorithm

Recursive Depth First Search:

bool visited[N]; void dfs(int i) { int j; visited[i] = true; // Mark node i as "visited" /* --------------------------------------------------------------- We reached node i... Something wonderful may happen at i I print node i out - Replace with code that solves your problem --------------------------------------------------------------- */ cout << i << endl; // Debug use /* --------------------------------------------------------------- How you find nodes j will depend on how you represent the graph --------------------------------------------------------------- */ for ( each node j that can be reached from node i ) { if ( ! visited[j] ) { dfs(j); // Visit node j } } }

How the DFS algorithm works

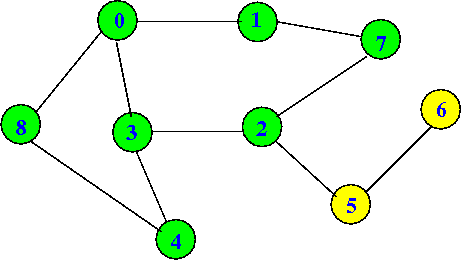
Suppose the graph is as follows

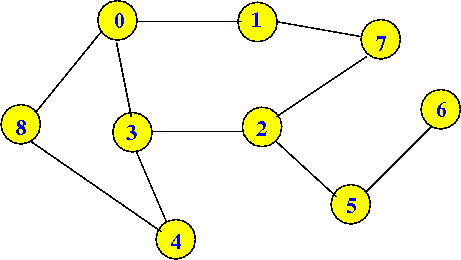
We start the graph traversal at node 0

How the DFS algorithm works

We call dfs(0):

dfs(0) visited[0] = F visited[1] = F visited[2] = F visited[3] = F visited[4] = F visited[5] = F visited[6] = F visited[7] = F visited[8] = F

How the DFS algorithm works

dfs(0) will set visited[0] = true:

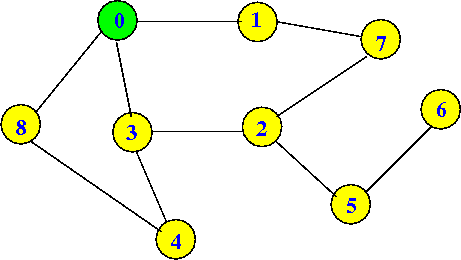
dfs(0) visited[0] = T visited[0] = T visited[1] = F visited[2] = F visited[3] = F visited[4] = F visited[5] = F visited[6] = F visited[7] = F visited[8] = F

How the DFS algorithm works

dfs(0) then visits all the unvisited reachable nodes with recursion:

dfs(0) visited[0] = T dfs(1) visited[1] = F dfs(3) visited[2] = F dfs(8) visited[3] = F visited[4] = F visited[5] = F visited[6] = F visited[7] = F visited[8] = F

How the DFS algorithm works

dfs(1) will run:

dfs(0) visited[0] = T dfs(1) -> dfs(1) runs visited[1] = F dfs(3) visited[2] = F dfs(8) visited[3] = F visited[4] = F visited[5] = F visited[6] = F visited[7] = F visited[8] = F

How the DFS algorithm works

dfs(1) will set visited[1] = true:

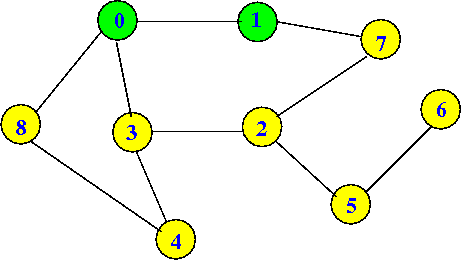
dfs(0) visited[0] = T dfs(1) -> dfs(1) runs visited[1] = T dfs(3) visited[2] = F dfs(8) visited[3] = F visited[4] = F visited[5] = F visited[6] = F visited[7] = F visited[8] = F

How the DFS algorithm works

dfs(1) then visits all the unvisited reachable nodes with recursion:

dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) visited[2] = F dfs(8) visited[3] = F visited[4] = F visited[5] = F visited[6] = F visited[7] = F visited[8] = F

How the DFS algorithm works

dfs(7) will run:

dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) runs visited[2] = F dfs(8) visited[3] = F visited[4] = F visited[5] = F visited[6] = F visited[7] = F visited[8] = F

How the DFS algorithm works

dfs(7) will set visited[7] = true:

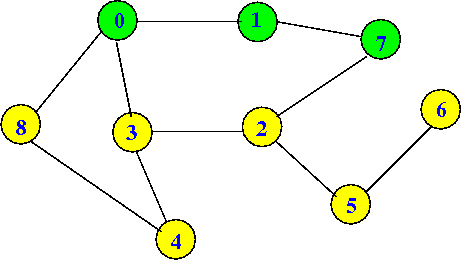
dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) runs visited[2] = F dfs(8) visited[3] = F visited[4] = F visited[5] = F visited[6] = F visited[7] = T visited[8] = F

How the DFS algorithm works

dfs(7) then visits all the unvisited reachable nodes with recursion:

dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = F dfs(8) dfs(2) visited[3] = F visited[4] = F visited[5] = F visited[6] = F visited[7] = T visited[8] = F

How the DFS algorithm works

dfs(2) will run:

dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = F dfs(8) dfs(2) -> dfs(2) runs visited[3] = F visited[4] = F visited[5] = F visited[6] = F visited[7] = T visited[8] = F

How the DFS algorithm works

dfs(2) will set visited[2] = true:

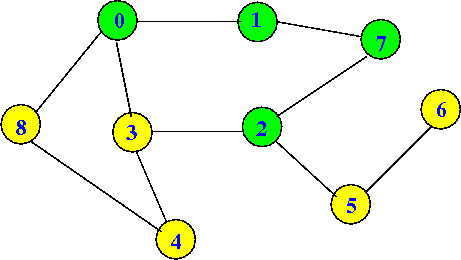
dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) runs visited[3] = F visited[4] = F visited[5] = F visited[6] = F visited[7] = T visited[8] = F

How the DFS algorithm works

dfs(2) then visits all the unvisited reachable nodes with recursion:

dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = F dfs(3) visited[4] = F dfs(5) visited[5] = F visited[6] = F visited[7] = T visited[8] = F

How the DFS algorithm works

dfs(3) will run:

dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = F dfs(3) -> dfs(3) runs visited[4] = F dfs(5) visited[5] = F visited[6] = F visited[7] = T visited[8] = F

How the DFS algorithm works

dfs(3) will set visited[3] = true:

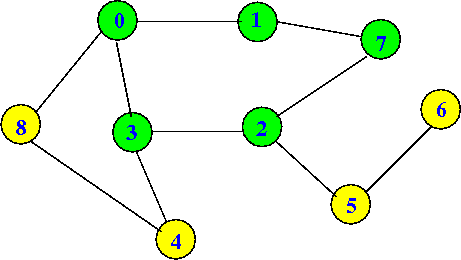
dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T dfs(3) -> dfs(3) runs visited[4] = F dfs(5) visited[5] = F visited[6] = F visited[7] = T visited[8] = F

How the DFS algorithm works

dfs(3) then visits all the unvisited reachable nodes with recursion:

dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T dfs(3) -> dfs(3) visited[4] = F dfs(5) dfs(4) visited[5] = F visited[6] = F visited[7] = T visited[8] = F

How the DFS algorithm works

dfs(4) will run:

dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T dfs(3) -> dfs(3) visited[4] = F dfs(5) dfs(4) visited[5] = F visited[6] = F visited[7] = T visited[8] = F

How the DFS algorithm works

dfs(4) will set visited[4] = true:

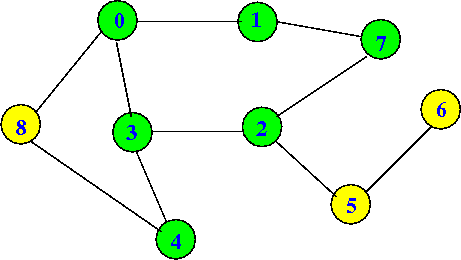
dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T dfs(3) -> dfs(3) visited[4] = T dfs(5) dfs(4) visited[5] = F visited[6] = F visited[7] = T visited[8] = F

How the DFS algorithm works

dfs(4) then visits all the unvisited reachable nodes with recursion:

dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T dfs(3) -> dfs(3) visited[4] = T dfs(5) dfs(4) visited[5] = F | visited[6] = F V visited[7] = T dfs(8) visited[8] = F

How the DFS algorithm works

dfs(8) will run:

dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T dfs(3) -> dfs(3) visited[4] = T dfs(5) dfs(4) visited[5] = F | visited[6] = F V visited[7] = T dfs(8) visited[8] = F

How the DFS algorithm works

dfs(8) will set visited[8] = true:

dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T dfs(3) -> dfs(3) visited[4] = T dfs(5) dfs(4) visited[5] = F | visited[6] = F V visited[7] = T dfs(8) visited[8] = T

How the DFS algorithm works

dfs(8) then visits all the unvisited reachable nodes with recursion:

dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T dfs(3) -> dfs(3) visited[4] = T dfs(5) dfs(4) visited[5] = F ^ visited[6] = F | visited[7] = T dfs(8) returns ! dfs(8) visited[8] = T

How the DFS algorithm works

dfs(4) will continue:

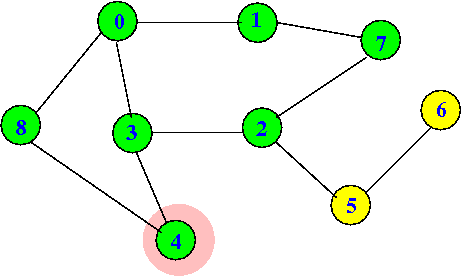
dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T dfs(3) -> dfs(3) visited[4] = T dfs(5) dfs(4) visited[5] = F visited[6] = F visited[7] = T visited[8] = F

How the DFS algorithm works

dfs(4) will continue:

dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T dfs(3) -> dfs(3) visited[4] = T dfs(5) dfs(4) visited[5] = F dfs(4) returns ! visited[6] = F visited[7] = T visited[8] = F

How the DFS algorithm works

dfs(3) will continue:

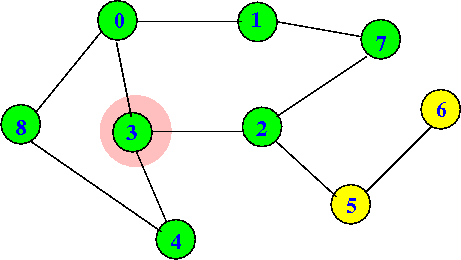
dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T dfs(3) -> dfs(3) visited[4] = T dfs(5) visited[5] = F visited[6] = F visited[7] = T visited[8] = F

How the DFS algorithm works

dfs(3) will continue:

dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T ~~dfs(3)~~ visited[4] = T dfs(5) visited[5] = F visited[6] = F dfs(3) returns ! visited[7] = T visited[8] = F

How the DFS algorithm works

dfs(2) will continue:

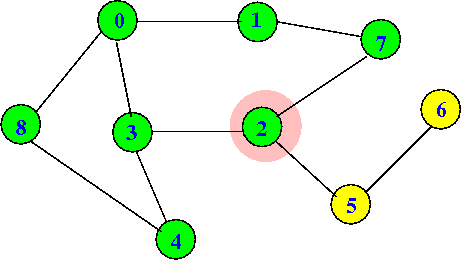
dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T ~~dfs(3)~~ visited[4] = T dfs(5) visited[5] = F visited[6] = F visited[7] = T visited[8] = F

How the DFS algorithm works

dfs(2) will call dfs(5) (the next unvisted node):

dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T ~~dfs(3)~~ visited[4] = T dfs(5) visited[5] = F visited[6] = F visited[7] = T visited[8] = F

How the DFS algorithm works

dfs(5) will run:

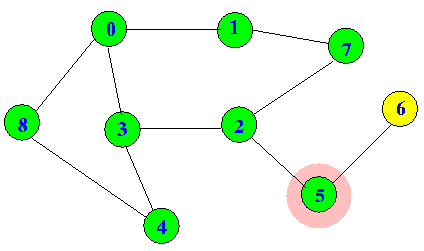
dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T ~~dfs(3)~~ visited[4] = T dfs(5) runs visited[5] = F visited[6] = F visited[7] = T visited[8] = F

How the DFS algorithm works

dfs(5) will set visited[5] = true:

dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T ~~dfs(3)~~ visited[4] = T dfs(5) runs visited[5] = T visited[6] = F visited[7] = T visited[8] = F

How the DFS algorithm works

dfs(5) then visits all the unvisited reachable nodes with recursion:

dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T ~~dfs(3)~~ visited[4] = T dfs(5) visited[5] = T | visited[6] = F V visited[7] = T dfs(6) visited[8] = F

How the DFS algorithm works

dfs(6) then runs:

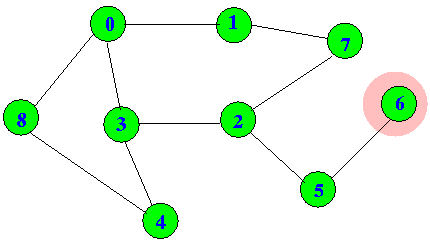
dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T ~~dfs(3)~~ visited[4] = T dfs(5) visited[5] = T | visited[6] = F V visited[7] = T dfs(6) visited[8] = F

How the DFS algorithm works

dfs(6) will sets visited[6] = true:

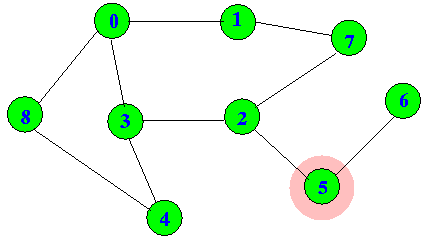
dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T ~~dfs(3)~~ visited[4] = T dfs(5) visited[5] = T | visited[6] = T V visited[7] = T dfs(6) visited[8] = F

How the DFS algorithm works

dfs(6) then returns to dfs(5):

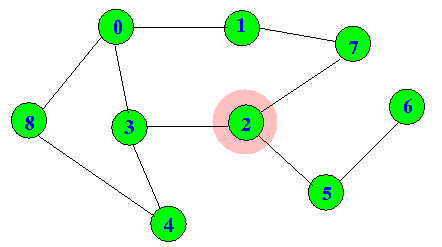
dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T ~~dfs(3)~~ visited[4] = T dfs(5) visited[5] = T ^ visited[6] = T | visited[7] = T ~~dfs(6)~~ visited[8] = F

How the DFS algorithm works

dfs(5) then returns to dfs(2):

dfs(0) visited[0] = T dfs(1) -> dfs(1) visited[1] = T dfs(3) dfs(7) -> dfs(7) visited[2] = T dfs(8) dfs(2) -> dfs(2) visited[3] = T ~~dfs(3)~~ visited[4] = T ~~dfs(5)~~ visited[5] = T ^ visited[6] = T | visited[7] = T ~~dfs(6)~~ visited[8] = F

And so on ---- Note: dfs(3) and dfs(8) will not be run because their visited[ ] value is true !