Data representation
The reachability of pages can be represented as a graph:
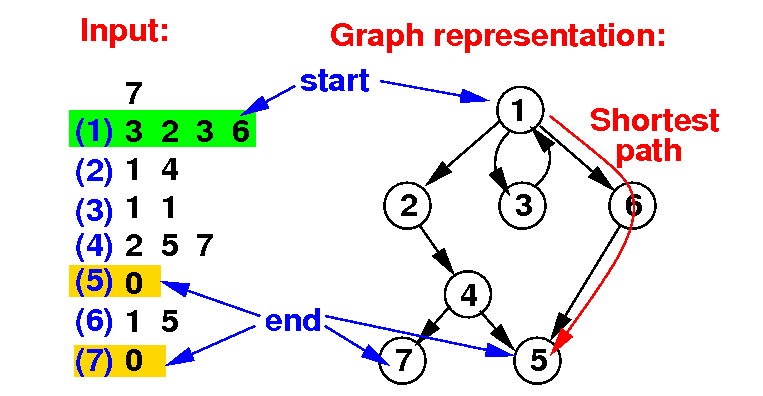
We always start at page 1 We end on a page with 0 entry. This is a classic shortest path problem. It is solved using the breath first search graph traversal algorithm |
Data representation
The graph can be represented by an adjacency list:
page[1] = {2, 3, 6} // page[i] = vector of pages reachable from page i
page[2] = {4}
page[3] = {1}
page[4] = {5, 7}
page[5] = {}
page[6] = {5}
page[7] = {}
|
Data representation
C++ code to read in the input:
vector<int> page[10001]; // page[i] = list of reachable pages
for ( int i = 1; i <= N; i++ )
{
int K;
cin >> K;
for ( int j = 0; j < K; j++ )
{
cin >> x;
page[i].push_back(x);
}
}
|
Breadth First Search Algorithm
This is the generic breath first search algorithm:
void bfs()
{
int i, j;
while ( myQueue != empty )
{
i = myQueue.remove(); // Get next node to visit
visited[i] = true; // Mark node i as "visited"
/* ----------------------------------------------------------
We reached node i... Something wonderful may happen at i
---------------------------------------------------------- */
cout << i << endl; // Change accordingly
/* -------------------------------------------------------------
How you find nodes j will depend on how you represent the graph
------------------------------------------------------------- */
for ( each node j that can be reached from node i )
{
if ( ! visited[j] )
{
myQueue.push(j); // Visit node j
} // When you loop back up, myQueue.pop() will visit the node!
}
}
}
|
Breadth First Search Algorithm
Adapt the queue operations to C++ syntax:
void bfs()
{
int i, j;
while ( ! myQueue.empty() )
{
i = myQueue.front(); myQueue.pop();
visited[i] = true; // Mark node i as "visited"
/* ----------------------------------------------------------
We reached node i... Something wonderful may happen at i
---------------------------------------------------------- */
cout << i << endl; // Change accordingly
/* -------------------------------------------------------------
How you find nodes j will depend on how you represent the graph
------------------------------------------------------------- */
for ( each node j that can be reached from node i )
{
if ( ! visited[j] )
{
myQueue.push(j); // Visit node j
} // When you loop back up, myQueue.pop() will visit the node!
}
}
}
|
Breadth First Search Algorithm
How do we visit the neighbors ??
void bfs()
{
int i, j;
while ( ! myQueue.empty() )
{
i = myQueue.front(); myQueue.pop();
visited[i] = true; // Mark node i as "visited"
/* ----------------------------------------------------------
We reached node i... Something wonderful may happen at i
---------------------------------------------------------- */
cout << i << endl; // Change accordingly
/* -------------------------------------------------------------
How you find nodes j will depend on how you represent the graph
------------------------------------------------------------- */
for ( each node j that can be reached from node i )
{
if ( ! visited[j] )
{
myQueue.push(j); // Visit node j
} // When you loop back up, myQueue.pop() will visit the node!
}
}
}
|
Breadth First Search Algorithm
Use the nodes listed in the adjacency list for page[i]:
void bfs()
{
int i, j;
while ( ! myQueue.empty() )
{
i = myQueue.front(); myQueue.pop();
visited[i] = true; // Mark node i as "visited"
/* ----------------------------------------------------------
We reached node i... Something wonderful may happen at i
---------------------------------------------------------- */
cout << i << endl; // Change accordingly
/* -------------------------------------------------------------
How you find nodes j will depend on how you represent the graph
------------------------------------------------------------- */
for ( int j = 0; j < page[i].size(); j++ )
{
if ( ! visited[ page[i][j] ] )
{
myQueue.push( page[i][j] ); // Visit page page[i][j]
} // When you loop back up, myQueue.pop() will visit the node!
}
}
}
|
Demo: CCC/2018/j5-ver1.cc
Output of j5-ver1.cc
The output printed by j5-ver1.cc:
|
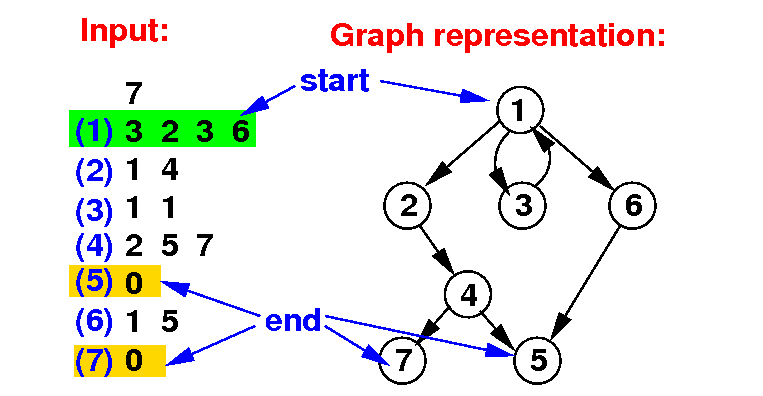
1
Push(2)
Push(3)
Push(6)
2
Push(4)
3
6
Push(5)
4
Push(5)
Push(7)
5
5
7
|
Output of j5-ver1.cc
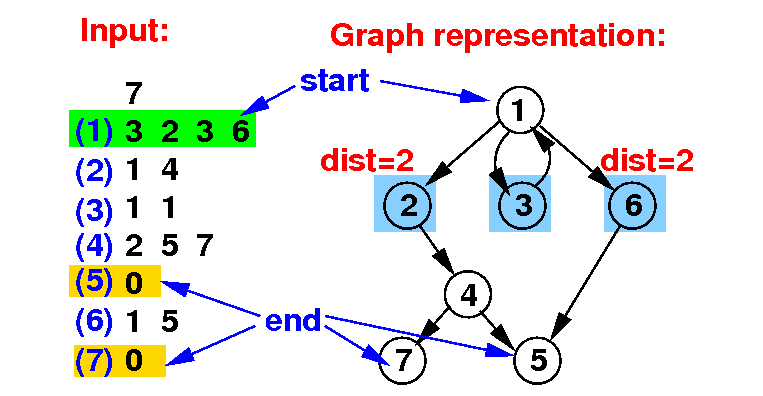
First, the closest nodes will be visited:
|
1
Push(2)
Push(3)
Push(6)
2
Push(4)
3
6
Push(5)
4
Push(5)
Push(7)
5
5
7
|
Output of j5-ver1.cc
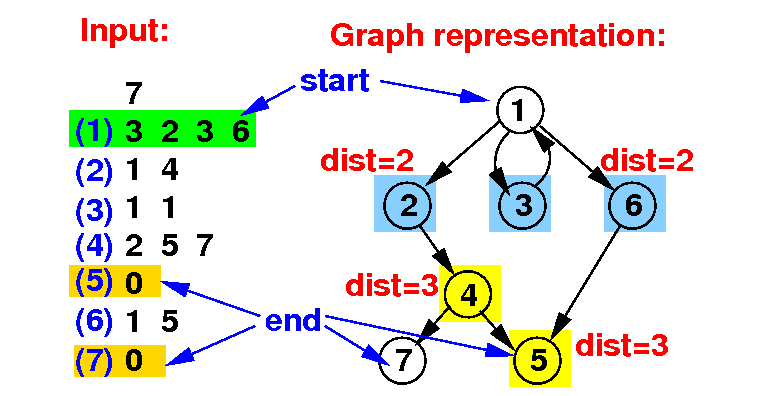
First, the next layer of nodes will be visited:
|
1
Push(2)
Push(3)
Push(6)
2
Push(4)
3
6
Push(5)
4
Push(5)
Push(7)
5
5
7
|
We visit
node 5 with
distance = 3
That is the shortest path !!!
We need to maintain
distance information
with each page !!!
Breadth First Search Algorithm
with distance information
Version 2: store page distance in another (parallel) queue distances:
void bfs()
{
int i, j, dist;
while ( ! myQueue.empty() )
{
i = myQueue.front(); myQueue.pop();
dist = distances.front(); distances.pop();
visited[i] = true; // Mark node i as "visited"
/* ----------------------------------------------------------
We reached node i... Something wonderful may happen at i
---------------------------------------------------------- */
cout << i << dist << endl; // Change accordingly
for ( int j = 0; j < page[i].size(); j++ )
{
if ( ! visited[ page[i][j] ] )
{
myQueue.push( page[i][j] ); // Visit page page[i][j]
distances.push( dist + 1 );
} // When you loop back up, myQueue.pop() will visit the node!
}
}
}
|
Demo: CCC/2018/j5-ver2.cc
Output of j5-ver2.cc
The output printed by j5-ver2.cc:
|
|
1(dist = 1)
push(2) 2
push(3) 2
push(6) 2
2(dist = 2)
push(4) 3
3(dist = 2)
6(dist = 2)
push(5) 3
4(dist = 3)
push(5) 4
push(7) 4
5(dist = 3)
5(dist = 4)
7(dist = 4)
|
Notice that the algorithm has found the shortest path length = 3 !!!
J5 solution in C++
void bfs()
{
int j;
while ( ! myQueue.empty() )
{
int i;
int dist;
/* ----------------------------------
Visit next node
---------------------------------- */
i = myQueue.front(); myQueue.pop();
dist = distances.front(); distances.pop();
visited[i] = true; // Mark node i as "visited"
/* ---------------------------------------------------------------
We reached node i... Something wonderful may happen at i
I print node i out - Replace with code that solves your problem
--------------------------------------------------------------- */
cout << ">> " << i << endl; // Debug use
/* --------------------------------------------
Check if page is terminal
-------------------------------------------- */
if ( page[i].size() == 0 ) // Terminal page
{
if ( dist < minPathLen )
{
minPathLen = dist ;
cout << " ** new shortest path length: " << minPathLen << endl;
}
}
/* ---------------------------------------------------------------
Visit pages reachable from page[i] that you have NOT visited
--------------------------------------------------------------- */
for ( int j = 0; j < page[i].size(); j++ )
{
if ( ! visited[ page[i][j] ] )
{
cout << " push(" << page[i][j] << ") " << dist+1 << endl;
myQueue.push( page[i][j] );
distances.push( dist + 1 );
}
}
}
}
|
Demo: CCC/2018/j5.cc