8 pieces of pie divided among 4 people:
1 1 1 5 1 2 2 3 2 2 2 2
1 1 2 4
1 1 3 3
9 pieces of pie divided among 4 people:
1 1 1 6 1 2 2 4 1 3 3 - 2 2 2 3
1 1 2 5 1 2 3 3
1 1 3 4
|
pie( nPieces, nPeople, min ) = # way to distribute nPieces of pie
among nPeople where each get a
minimum of min pieces
The recusrive property of this problem becomes clear with a larger example.
Divide 13 pieces among 4 people:
1 1 1 10 1 2 2 8 1 3 3 6 1 4 4 4
1 1 2 9 1 2 3 7 1 3 4 5
1 1 3 8 1 2 4 6
1 1 4 7 1 2 5 5
1 1 5 6
2 2 2 7 2 3 3 5
2 2 3 6 2 3 4 4
2 2 4 5
3 3 3 4
|
pie( nPieces, nPeople, min ) = # way to distribute nPieces of pie
among nPeople where each get a
minimum of min pieces
The recusrive property of this problem becomes clear with a larger example.
Divide 13 pieces among 4 people:
Give 1 pie to person 1 and divide 12 pieces among 3 people:
1 1 1 10 1 2 2 8 1 3 3 6 1 4 4 4
1 1 2 9 1 2 3 7 1 3 4 5
1 1 3 8 1 2 4 6
1 1 4 7 1 2 5 5 (Note: each of them must get ≥ 1 piece)
1 1 5 6
Give 2 pies to person 1 and divide 11 pieces among 3 people:
2 2 2 7 2 3 3 5
2 2 3 6 2 3 4 4 (Note: each of them must get ≥ 2 pieces)
2 2 4 5
Give 3 pies to person 1 and divide 10 pieces among 3 people:
3 3 3 4 (Note: each of them must get ≥ 3 pieces)
|
Where is the recursion ? Divide 13 pieces among 4 people: (1) Give 1 pie to person 1 and divide 12 pieces among 3 people: 1 1 1 10 1 2 2 8 1 3 3 6 1 4 4 4 1 1 2 9 1 2 3 7 1 3 4 5 1 1 3 8 1 2 4 6 1 1 4 7 1 2 5 5 (Note: each of them must get ≥ 1 piece) 1 1 5 6 |
Where is the recursion ? Divide 13 pieces among 4 people: (1) Give 1 pie to person 1 and divide 12 pieces among 3 people: 1 1 1 10 1 2 2 8 1 3 3 6 1 4 4 4 1 1 2 9 1 2 3 7 1 3 4 5 1 1 3 8 1 2 4 6 1 1 4 7 1 2 5 5 (Note: each of them must get ≥ 1 piece) 1 1 5 6 Ways to divide 12 pieces among 3 people: 1 1 10 2 2 8 3 3 6 4 4 4 1 2 9 2 3 7 3 4 5 1 3 8 2 4 6 1 4 7 2 5 5 (Note: each of them must get ≥ 1 piece) 1 5 6 This is a smaller version of the same type of problem !!! |
Where is the recursion ? Divide 13 pieces among 4 people: (2) Give 2 pies to person 1 and divide 11 pieces among 3 people: 2 2 2 7 2 3 3 5 2 2 3 6 2 3 4 4 (Note: each of them must get ≥ 2 piece) 2 2 4 5 |
Where is the recursion ? Divide 13 pieces among 4 people: (2) Give 2 pies to person 1 and divide 11 pieces among 3 people: 2 2 2 7 2 3 3 5 2 2 3 6 2 3 4 4 (Note: each of them must get ≥ 2 piece) 2 2 4 5 Ways to divide 11 pieces among 3 people: 2 2 7 3 3 5 2 3 6 3 4 4 (Note: each of them must get ≥ 2 piece) 2 4 5 This is a smaller version of the same type of problem !!! |
Where is the recursion ? Divide 13 pieces among 4 people: (3) Give 3 pies to person 1 and divide 10 pieces among 3 people: 3 3 3 4 (Note: each of them must get ≥ 3 pieces) |
Where is the recursion ? Divide 13 pieces among 4 people: (3) Give 3 pies to person 1 and divide 10 pieces among 3 people: 3 3 3 4 (Note: each of them must get ≥ 3 pieces) Ways to divide 10 pieces among 3 people: 3 3 4 (Note: each of them must get ≥ 3 pieces) This is a smaller version of the same type of problem !!! |
Suppose we need to solve a problem of size n:
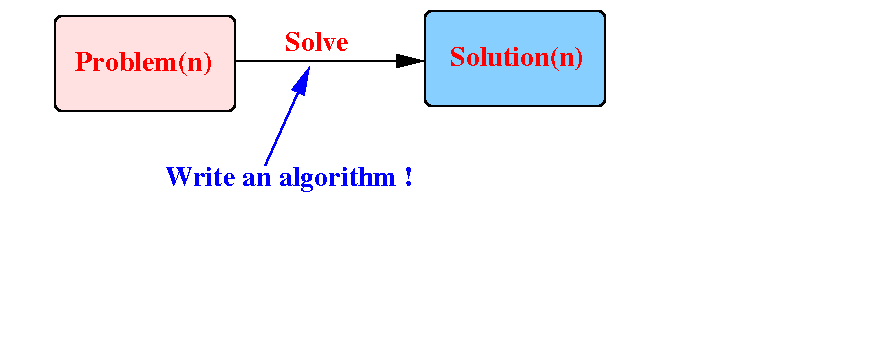
Consider the other identical (but) smaller problems:
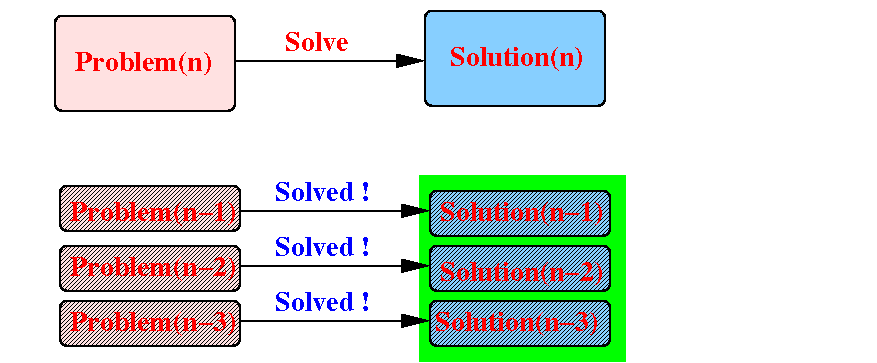
Suppose that we (already) have the solutions for all the smaller problems, i.e.: we do not need to solve them
If we can construct Solution(n) using the solutions of the smaller problems:
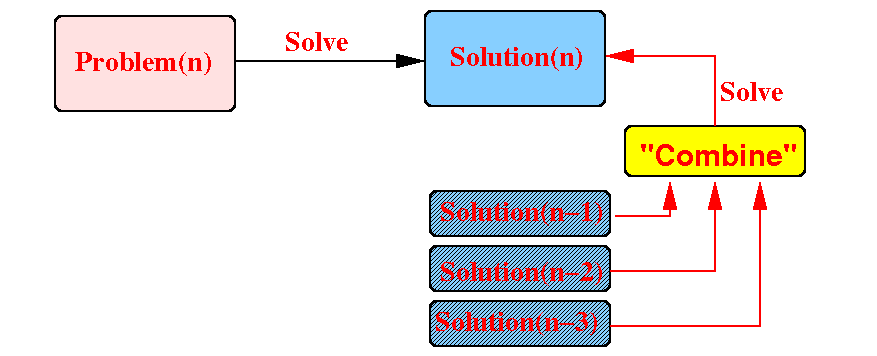
Then: we can use recursion to solve Problem(n) !!!
solution solveProb( P(n) )
{
if ( P(n) is a base case )
{
return solution constructed by you;
// Note: there can be many base cases !
}
else
{
// Solve smaller problems to help you
// find solution for P(n)
sol1 = solveProb( P(n-1) );
sol2 = solveProb( P(n-2) );
...
mySolution = combine( sol1, sol2, .... );
return mySolution;
}
|
Flesh out of the recusive part first...
int divPie(nPieces, nPeople, min)
{
if ( P(n) is a base case )
{
return solution constructed by you;
// Note: there can be many base cases !
}
else
{
// Give i pieces to person 1 and
// distr nPieces-i to nPeople-1 people
// where each get at least i pieces
for ( i = min; i <= nPieces/nPeople; i++ )
{
helpSol = divPie(nPieces-i, nPeople-1, i);
}
mySolution = sum all the helpSol values
return mySolution;
}
|
What are the bases cases ???
int divPie(nPieces, nPeople, min)
{
if ( nPerson == 1 )
{
Give him nPieces (only 1 way )
}
else
{
// Give i pieces to person 1 and
// distr nPieces-i to nPeople-1 people
// where each get at least i pieces
for ( i = min; i <= nPieces/nPeople; i++ )
{
helpSol = divPie(nPieces-i, nPeople-1, i);
}
mySolution = sum all the helpSol values
return mySolution;
}
|
int divPie(int nPieces, int nPeople, int min)
{
if ( nPeople == 1 )
{
return 1; // One way: this person gets nPieces
}
else
{
int nTotSols = 0, nSubSols;
for ( int i = min; i <= nPieces/nPeople; i++ )
{
// Give person 1: i pies, then divide nPieces-i pies among others
nSubSols = divPie( nPieces-i, nPeople-1, i);
nTotSols = nTotSols + nSubSols;
}
return nTotSols;
}
}
|
Problem: runs too slow for n=120 and k=20...