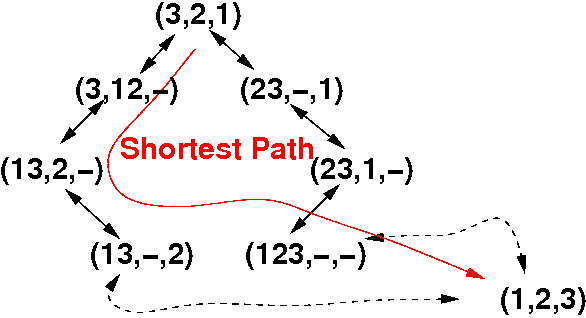
Overview
|
State representation
the state of a board
The problem starts with start with 1 coin in each spot of the board:
3 2 1 (3 coins)
Number of spots on the board is variable:
2 1 (2 coins)
So we must use a variable length array (= vector) to represent
the spots on the board:
vector< ??? > board;
where ??? represents the state in 1 spot on the board.
|
State representation
the state of a spot (on a board)
We start with 1 coin in each spot of the board:
3 2 1 (3 coins)
But: we can move a smaller coin "on top" on a larger coin:
3 2 1 ---> 3 12 -
^ |
| |
+---+
Therefore: each spot can contain a variable number of coins !!!
So we must use a variable length array (= vector) to represent
the state of a spot on the board:
---> vector< vector < int > > board; !!!
|
Data structure used for BFS
The queues:
queue< vector< vector
|
Initialization
queue< vector< vector
|
Breadth First Search Algorithm
void bfs()
{
int i, j;
while ( myQueue != empty )
{
i = myQueue.remove(); // Get next node to visit
visited[i] = true; // Mark node i as "visited"
/* ----------------------------------------------------------
We reached node i... Something wonderful may happen at i
---------------------------------------------------------- */
cout << i << endl; // Change accordingly
/* -------------------------------------------------------------
How you find nodes j will depend on how you represent the graph
------------------------------------------------------------- */
for ( each node j that can be reached from node i )
{
if ( ! visited[j] )
{
myQueue.push(j); // Visit node j
} // When you loop back up, myQueue.pop() will visit the node!
}
}
}
|
BFS:
processing a board (we reached node i...)
/* ----------------------------------------------------------
We reached node i... Something wonderful may happen at i
---------------------------------------------------------- */
board = q.front(); q.pop();
dist = d.front(); d.pop();
visited[board] = true;
if ( finished(board) )
{
cout << "\nAnswer: " << dist << endl;
exit(0);
}
|
How do we tell if the state of the board is the end state ?
How to test for a solution ?
/* --------------------------------------------------
Check is board is done: 1 2 3 4 ... N
Check for:
(1) Each spot has 1 coin
(2) Spot i has coin i+1
-------------------------------------------------- */
bool finished( vector< vector< int> > board )
{
for ( int i = 0; i < board.size(); i++)
{
if ( board[i].size() != 1 ) // more than 1 coin in a spot
return false;
else if ( board[i][0] != i+1 ) // coin i is not in its position
return false;
}
return true;
}
|
Breadth First Search Algorithm
void bfs()
{
int i, j;
while ( myQueue != empty )
{
i = myQueue.remove(); // Get next node to visit
visited[i] = true; // Mark node i as "visited"
/* ----------------------------------------------------------
We reached node i... Something wonderful may happen at i
---------------------------------------------------------- */
cout << i << endl; // Change accordingly
/* -------------------------------------------------------------
How you find nodes j will depend on how you represent the graph
------------------------------------------------------------- */
for ( each node j that can be reached from node i )
{
if ( ! visited[j] )
{
myQueue.push(j); // Visit node j
} // When you loop back up, myQueue.pop() will visit the node!
}
}
}
|
BFS:
making the next step
on the board
|
BFS:
moving a coin to the
right spot
on the board
/* ---------------------------------------------------------
Check if we can move a coin from slot i --> i+1
--------------------------------------------------------- */
for ( int i = 0; i < board.size()-1; i++ )
{
// Make sure there is some coin in slot i for you to move !
if ( board[i].size() == 0 )
continue;
if ( board[i+1].size() == 0 // slot i empty --> move OK
|| board[i][0] < board[i+1][0] // coin in slot i is SMALLER --> OK
)
{
Make newBoard by moving top coin in slot i to slot i+1
if ( !visited[newBoard] )
{
q.push( newBoard );
d.push( dist+1 );
}
}
|
Do the same for a left move and we are done !
Sample output for J5
3 : 2 : 1 : ---> 0 (Initial state)
<-- 3 : 12 : : ---> 1
<-- 23 : : 1 : ---> 1
<-- 13 : 2 : : ---> 2
<-- 23 : 1 : : ---> 2
--> 13 : : 2 : ---> 3
<-- 123 : : : ---> 3
--> 3 : 1 : 2 : ---> 4
--> 3 : : 12 : ---> 5
--> : 3 : 12 : ---> 6
<-- : 13 : 2 : ---> 7
<-- 1 : 3 : 2 : ---> 8
<-- 1 : 23 : : ---> 9
--> : 123 : : ---> 10
--> : 23 : 1 : ---> 11
<-- 2 : 3 : 1 : ---> 12
<-- 2 : 13 : : ---> 13
<-- 12 : 3 : : ---> 14
--> 12 : : 3 : ---> 15
--> 2 : 1 : 3 : ---> 16
--> 2 : : 13 : ---> 17
--> : 2 : 13 : ---> 18
<-- : 12 : 3 : ---> 19
<-- 1 : 2 : 3 : ---> 20
Answer: 20
|