Data representation

 

  • The invite relationship can be represented as a tree (with root = Mark)

    Example: 

       Sample input:             Invite tree
 =============            ==============      
      4  (=Mark)                4
  (1) 3                        / \
  (2) 4	                      2   3
  (3) 4                           |
				  1

  • This problem tests if you can count # different ways to prune this tree

Problem analysis

 

  • Number of ways to un-invite Mark's friends:

              

  • This counting problem is recursive (because trees have subtrees)

Problem analysis   why is this counting problem recursive

  • Suppose this is the original invite tree: 

                          7
                  /  \
		 6    5
		/ \   |
	       3   4  2
               |
	       1

  • You have these subtrees that have identical nature (counted the same way): 

             6                           5
      / \                          |
     3   4                         2
     |
     1

Finding the recursive relationship

  • Let's find all the subsets of friends than can be uninvited for these subtrees: 

             6                           5             
      / \                          |            
     3   4                         2
     |
     1

Finding the recursive relationship

  • These are the possible subsets of friends: 

             6       {}                  5      {} 
      / \      {1} {13}            |      {2}
     3   4     {4}                 2      {25}
     |         {14} {134}
     1         {1346}

(I included the universe set in red because it will be important as shown next)

Finding the recursive relationship 

             6       {}                  5      {} 
      / \      {1} {13}            |      {2}
     3   4     {4}                 2      {25}
     |         {14} {134}
     1         {1346}

  • How can we use the above result to solve subsets in this tree: 

                7             
        /  \		
       6    5           
      / \   |         
     3   4  2          
     |                 
     1

Finding the recursive relationship 

             6       {}                  5      {} 
      / \      {1} {13}            |      {2}
     3   4     {4}                 2      {25}
     |         {14} {134}
     1         {1346}

  • (1) all the sets in tree 1 + { }: 

                7    {} {1} {13} {4} {14} {134} {1346}   
        /  \		
       6    5           
      / \   |         
     3   4  2          
     |                 
     1

Finding the recursive relationship 

             6       {}                  5      {} 
      / \      {1} {13}            |      {2}
     3   4     {4}                 2      {25}
     |         {14} {134}
     1         {1346}

  • (2) all the sets in tree 1 + {2}: 

                7    {} {1} {13} {4} {14} {134} {1346}   
        /  \   {2} {21} {213} {24} {214} {2134} {21346}
       6    5           
      / \   |         
     3   4  2          
     |                 
     1

Finding the recursive relationship 

             6       {}                  5      {} 
      / \      {1} {13}            |      {2}
     3   4     {4}                 2      {25}
     |         {14} {134}
     1         {1346}

  • (3) all the sets in tree 1 + {25}: 

                7    {} {1} {13} {4} {14} {134} {1346}   
        /  \   {2} {21} {213} {24} {214} {2134} {21346}
       6    5  {25} {251} {2513} {254} {2514} {25134} {251346}
      / \   |         
     3   4  2          
     |                 
     1

Finding the recursive relationship 

             6       {}                  5      {} 
      / \      {1} {13}            |      {2}
     3   4     {4}                 2      {25}
     |         {14} {134}
     1         {1346}

  • (4) To make the recusive relation work, we must include the whole tree: 

                7    {} {1} {13} {4} {14} {134} {1346}   
        /  \   {2} {21} {213} {24} {214} {2134} {21346}
       6    5  {25} {251} {2513} {254} {2514} {25134} {251346}
      / \   |  {1234567}       
     3   4  2          
     |         (We must include it because we
     1          started with subsets derived
                from full trees - see above !)

Finding the recursive relationship 

             6       {}                  5      {} 
      / \      {1} {13}            |      {2}
     3   4     {4}                 2      {25} (3 subsets)
     |         {14} {134}
     1         {1346} (7 subsets)

  • $64,000 question: what is the relationship ? 

                7    {} {1} {13} {4} {14} {134} {1346}   
        /  \   {2} {21} {213} {24} {214} {2134} {21346}
       6    5  {25} {251} {2513} {254} {2514} {25134} {251346}
      / \   |  {1234567}       
     3   4  2          
     |         
     1

Finding the recursive relationship 

             6       {}                  5      {} 
      / \      {1} {13}            |      {2}
     3   4     {4}                 2      {25} (3 subsets)
     |         {14} {134}
     1         {1346} (7 subsets)

  • Answer: 

                7    {} {1} {13} {4} {14} {134} {1346}   
        /  \   {2} {21} {213} {24} {214} {2134} {21346}
       6    5  {25} {251} {2513} {254} {2514} {25134} {251346}
      / \   |  {1234567}       
     3   4  2          
     |         
     1            # subsets = 3 × 7 + 1

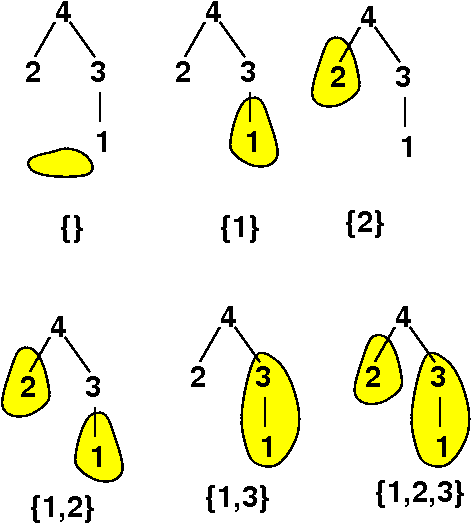
A larger example to show the recursive relationship of subsets

# subsets (including the universe set) = k1*k2*...*kN + 1 

                           Sets to remove                        How to form
                          ====================================  ==============
              7            {} {1} {2} {12} {126}                (R1=T(6)+{ }+{  })
         /    |    \       {5} {15} {25} {125} {1265}           (R2=T(6)+{5}+{  })
        6     5     4      {3} {13} {23} {123} {1263}           (R3=T(6)+{ }+{3 })
       / \          |      {53} {153} {253} {1253} {12653}      (R4=T(6)+{5}+{3 })
      1   2         3      {34} {134} {234} {1234} {12634}      (R5=T(6)+{ }+{34})
                           {534} {1534} {2534} {12534} {126534} (R6=T(6)+{5}+{34})
			   {1234567}
                           Total = 5 * 2 * 3 + 1

        6      {} {1} {2}         5   {}            4    {} {3}
       / \     {12}                   {5}           |    {34}
      1   2    {126}                                3
               Total = 2*2+1 = 5      Total = 2          Total = 2+1 = 3

      1  {}     2  {}                               3  {}
         {1}       {2}                                 {3}
         Total = 2 Total = 2                           Total = 2

where: k1, k2, k3 are the size of the subsets in the subtrees

Data representation

  

   4  <---- Mark = 4                     4
   3  <---- 3 invited 1                 / \
   4  <---- 4 invited 2                2   3
   4  <---- 4 invited 3                     \
                                             1

 Data repr:

        invited[4] = {2,3}
        invited[3] = {1}
        invited[2] = {}
        invited[1] = {}

 Use: (variable length array)

      vector<int> invited[10];   // Because N <= 6

Data representation

  

   4  <---- Mark = 4                     4
   3  <---- 3 invited 1                 / \
   4  <---- 4 invited 2                2   3
   4  <---- 4 invited 3                     \
                                             1
 Data repr:

        invited[4] = {2,3}
        invited[3] = {1}
        invited[2] = {}
        invited[1] = {}



   cin >> N;      // N = Mark, # Friends = N-1

   for ( int i = 1; i <= N-1; i++ )
   {
      cin >> k;  // Person i was invited in by person k
      invited[k].push_back(i); // Person k invites in person i
   }

J5 solution 

int countComb( vector x)
{
   int r = 1;
   int tmp;

   /* -------------------------
      Base case: no subtree
      ------------------------- */
   if ( x.size() == 0 )
      return 1+1;     // {} and {x}

   // Count the subtrees and multiply
   for ( int i = 0; i < x.size(); i++ )
   { 
      tmp =  countComb( invited[ x[i] ]);
      r *= tmp;
   }

   return r + 1;
}

int ans = countComb( invited[N] );
cout << ans-1 << endl;  // Adjust: can't uninvite Mark himself