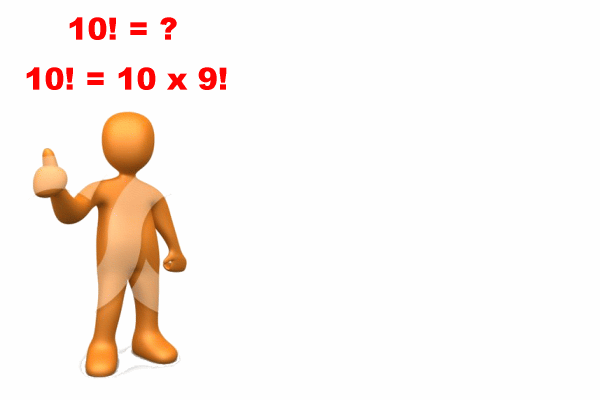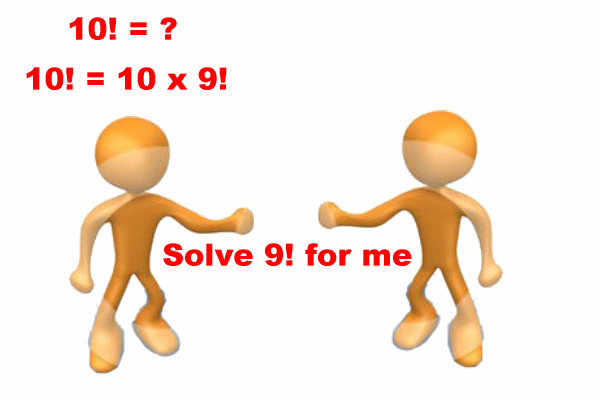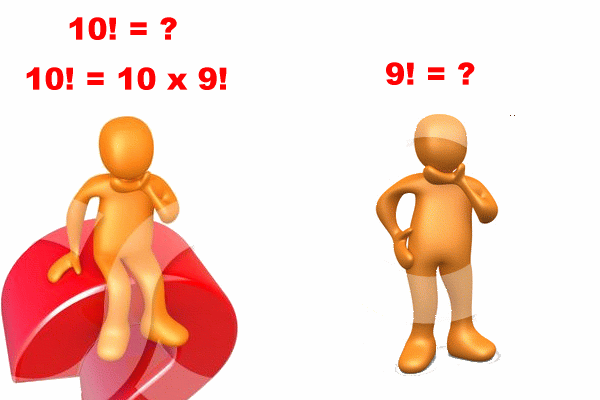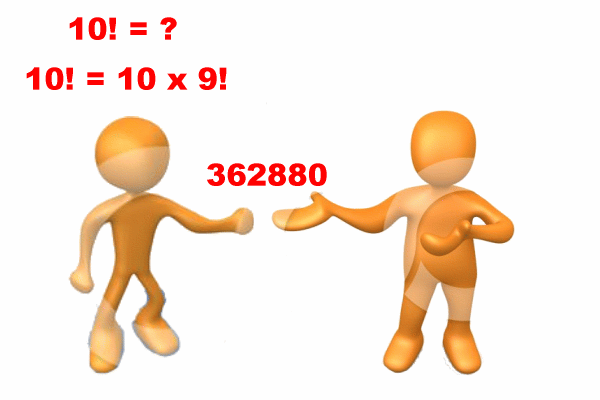A graphical presentation of
recursion as a
divide-and-conquer technique
|
A graphical presentation of
recursion as a
divide-and-conquer technique
|
A graphical presentation of
recursion as a
divide-and-conquer technique
|
A graphical presentation of
recursion as a
divide-and-conquer technique
|
A graphical presentation of
recursion as a
divide-and-conquer technique
|
A graphical presentation of
recursion as a
divide-and-conquer technique
|