The Tower of Hanoi problem/game

  • The Tower of Hanoi problem:

      • 3 pegs

      • A number of disks is stacked on peg 1

      • All disks have distinct sizes

      • Move all disks from peg 1 to peg 3 by:

        • Moving one disk at a time from any peg to any other peg
        • A disk cannot be placed on top of a smaller disk

The Tower of Hanoi problem/game

  • Watch how to solve the Tower of Hanoi with 4 disks:

      1. There are 3 towers labeled 1, 2 and 3.

      2. Initially, all the N disks are placed on tower 1

      3. Move only one disk at a time

      4. A disk cannot be moved on top of a smaller disk

Try it yourself: https://www.mathsisfun.com/games/towerofhanoi.html

Review:    When can we use recursion to solve a problem ?
 

If we can use the solutions of some smaller problems to find Solution(n) (= solution of original problem):

 
 

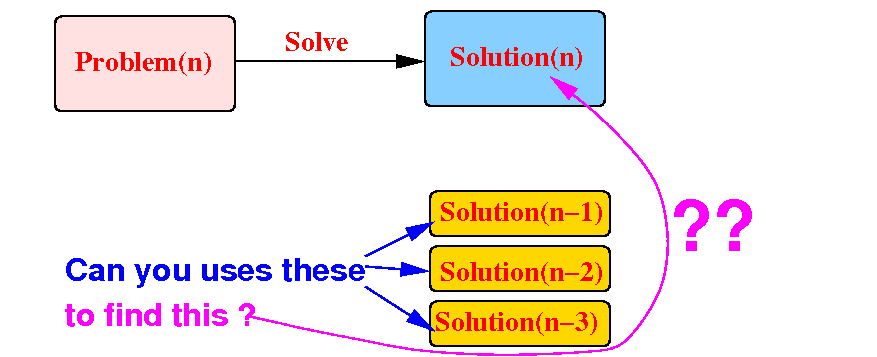
Then:   we can use recursion to solve the Problem(n)

Finding smaller Hanoi problems to help solve a bigger Hanoi problem
 

Problem(n, 1, 3, 2) = moving n disks from peg 1 to peg 3 with the help of peg 2:

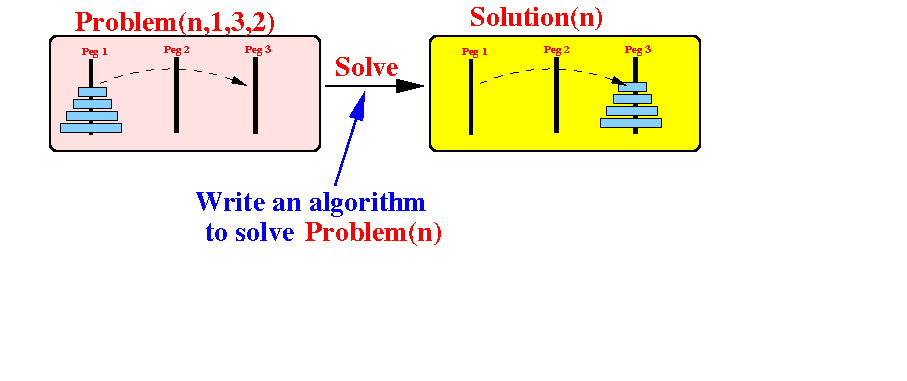
Question:   which smaller Hanoi problem(s) can be used to solve the Problem(n, 1, 3, 2)?

Finding smaller Hanoi problems to help solve a bigger Hanoi problem
 

Problem(n, 1, 3, 2) = moving n disks from peg 1 to peg 3 with the help of peg 2:

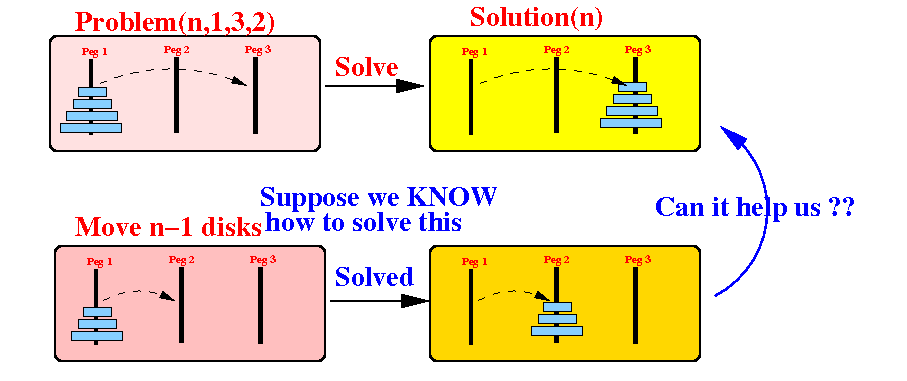
Suppose:   we can move (n−1) disks from any peg to any other peg

Can we use this knowledge to solve the original problem (that has n disks)?

Solving Hanoi(4 disks) using Hanoi(3 disks)
 

Consider moving 4 disks from peg 1 to peg 3 with the help of peg 2:

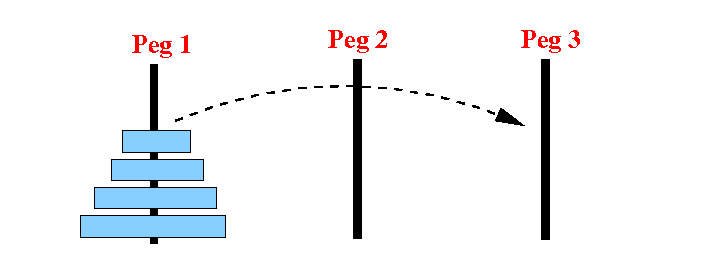
Suppose:   we can move 3 disks from any peg to any other peg

Can we use this knowledge to solve the original problem (that has 4 disks)?

Solving Hanoi(4 disks) using Hanoi(3 disks)
 

Step 1: move 3 disks from peg 1 to peg 2 with the help of peg 3:

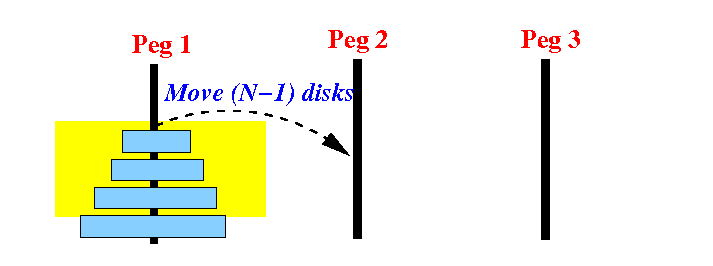
Note:   do not overthink and try to find this solution (don't worry about how to move the 3 disks)

Remember:   in recursion, we assume that we know/have the solution already

Solving Hanoi(4 disks) using Hanoi(3 disks)
 

Result:

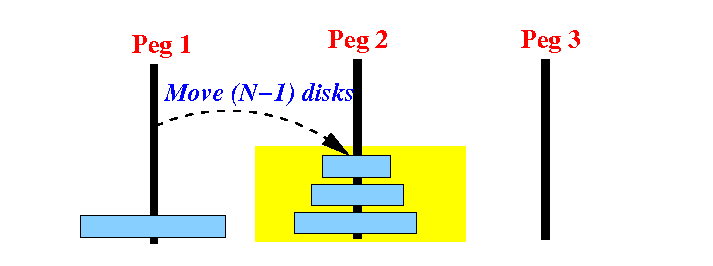
Can you see what we must do next ???

Solving Hanoi(4 disks) using Hanoi(3 disks)
 

Step 2: move 1 disk from peg 1 to peg 3 directly:

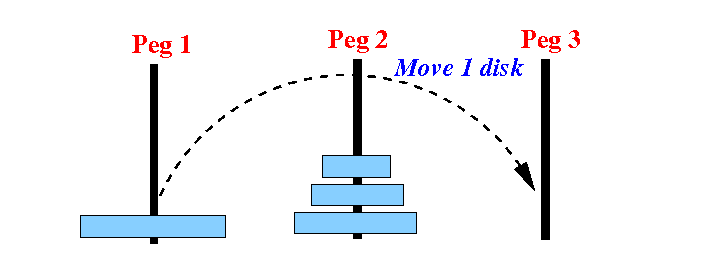
Note:   this step is easy (= a base case) because there is no disk on top of the last disk

Solving Hanoi(4 disks) using Hanoi(3 disks)
 

Result:

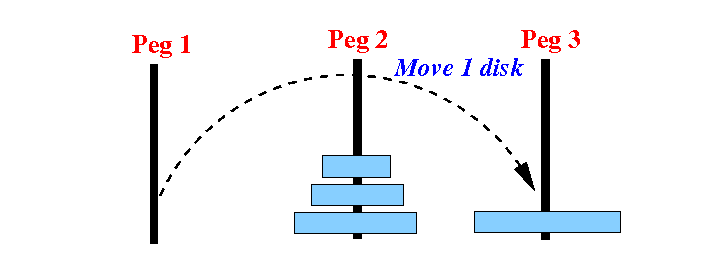
Can you see what we must do next ???

Solving Hanoi(4 disks) using Hanoi(3 disks)
 

Step 3: move 3 disks from peg 2 to peg 3 with the help of peg 1:

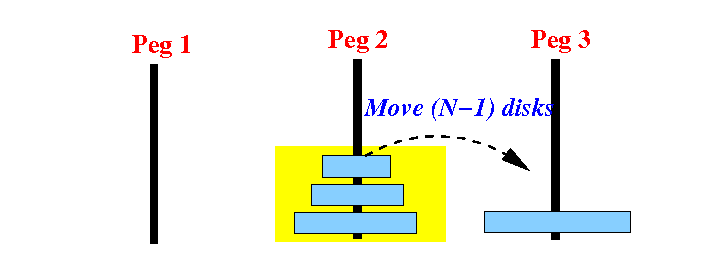
Again:   do not overthink and try to find this solution (don't worry about how to move the 3 disks)

Remember:   in recursion, we assume that we know/have the solution already

Solving Hanoi(4 disks) using Hanoi(3 disks)
 

Final result:

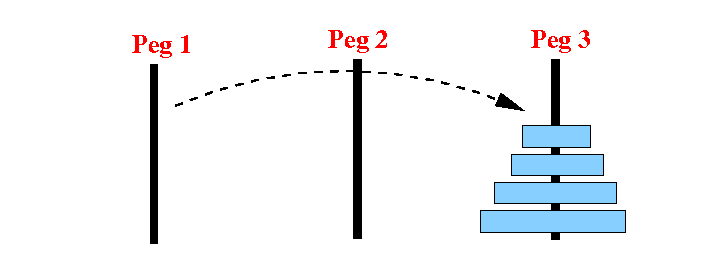
Solved ! all 4 disks have been moved from peg 1 to peg 3

Finding smaller Hanoi problems   revisited
 

Problem(n, 1, 3, 2) = moving n disk from peg 1 to peg 3 with the help of peg 2:

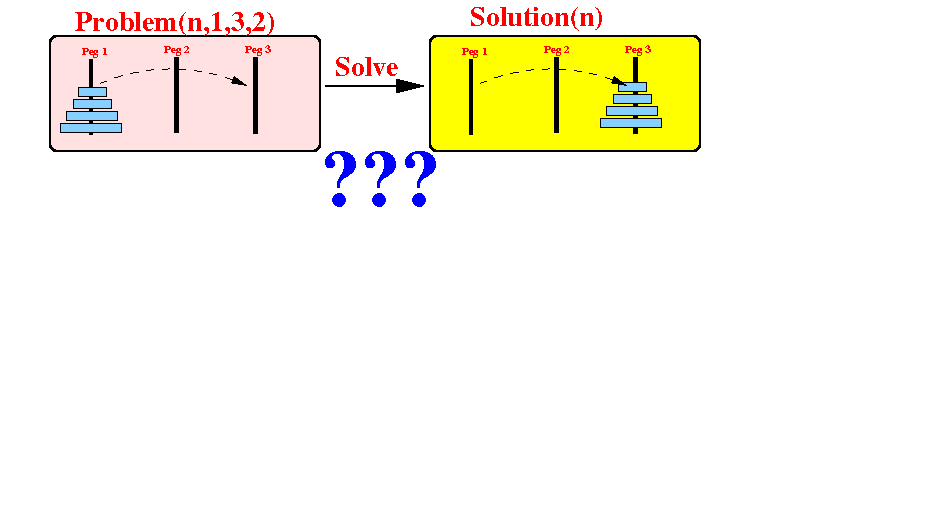
Question:   which smaller Hanoi problem(s) did we use to solve the Problem(n, 1, 3, 2)?

Finding smaller Hanoi problems   revisited
 

Problem(n, 1, 3, 2) = moving n disk from peg 1 to peg 3 with the help of peg 2:

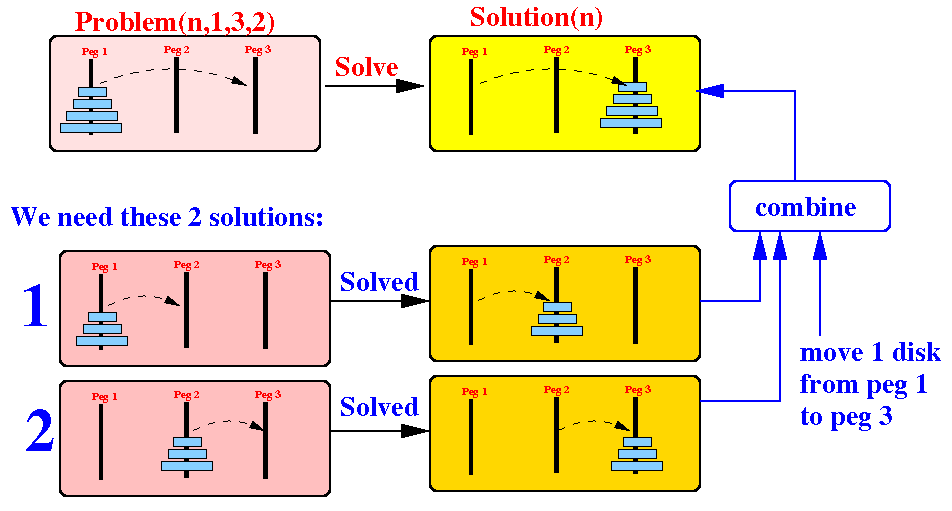
Answer:   Problem(n−1, 1, 2, 3) and the Problem(n−1, 2, 3, 1)

The hanoi(n, fr, to, h) method

The hanoi(n, fr, to, h) method will return instructions (as text) to move n disks from starting peg fr to destination peg to using help peg h 

    // Move n disks from peg fr to peg to with help of peg h

    public static String hanoi(int n, int fr, int to, int h)
    {
        if ( n == 1 )
	{  // base case
	   return fr + " --> " + to + "\n";
	}
	Returns instructions on how to move n disks
	from peg fr to peg to with the help of peg h

	    String helpSol1 = hanoi(n-1, fr, h, to);
	    String helpSol2 = hanoi(n-1, h, to, fr);
	    String myMove = fr + " --> " + to + "\n";

	    String mySol = helpSol1 + myMove + helpSol2;	    
	    return mySol;
        }
    }

The hanoi(n, fr, to, h) method

Base case:   moving 1 disk (from any peg to any other peg) is easy
Returns:   the text "from peg # --> to peg #" 

    // Move n disks from peg fr to peg to with help of peg h

    public static String hanoi(int n, int fr, int to, int h)
    {
        if ( n == 1 )
	{  // base case
	   return fr + " --> " + to + "\n";
	}
	else
	{
	    String helpSol1 = hanoi(n-1, fr, h, to);
	    String helpSol2 = hanoi(n-1, h, to, fr);
	    String myMove = fr + " --> " + to + "\n";

	    String mySol = helpSol1 + myMove + helpSol2;
	    
	    return mySol;
        }
    }

The hanoi(n, fr, to, h) method

Recursive case:   moving n disk will use the solutions from 2 smaller Hanoi problems:
  

    // Move n disks from peg fr to peg to with help of peg h

    public static String hanoi(int n, int fr, int to, int h)
    {
        if ( n == 1 )
	{  // base case
	   return fr + " --> " + to + "\n";
	}
	else
	{
	    String helpSol1 = hanoi(n-1, fr, h, to);
	    String helpSol2 = hanoi(n-1, h, to, fr);
	    String myMove = fr + " --> " + to + "\n";

	    String mySol = helpSol1 + myMove + helpSol2;
	    
	    return mySol;
        }
    }

The hanoi(n, fr, to, h) method

In addition, we need to move a disk from fr peg to to peg:
  

    // Move n disks from peg fr to peg to with help of peg h

    public static String hanoi(int n, int fr, int to, int h)
    {
        if ( n == 1 )
	{  // base case
	   return fr + " --> " + to + "\n";
	}
	else
	{
	    String helpSol1 = hanoi(n-1, fr, h, to);
	    String helpSol2 = hanoi(n-1, h, to, fr);
	    String myMove = fr + " --> " + to + "\n";

	    String mySol = helpSol1 + myMove + helpSol2;
	    
	    return mySol;
        }
    }

The hanoi(n, fr, to, h) method

Put all instructions in the correct order:
     (1) do steps in helpSol1, then (2) do myMove and finally (3) do steps in helpSol2 

    // Move n disks from peg fr to peg to with help of peg h

    public static String hanoi(int n, int fr, int to, int h)
    {
        if ( n == 1 )
	{  // base case
	   return fr + " --> " + to + "\n";
	}
	else
	{
	    String helpSol1 = hanoi(n-1, fr, h, to);
	    String helpSol2 = hanoi(n-1, h, to, fr);
	    String myMove = fr + " --> " + to + "\n";

	    String mySol = helpSol1 + myMove + helpSol2;
	    
	    return mySol;
        }
    }

The hanoi(n, fr, to, h) method

Return the instructions in mySol:
  

    // Move n disks from peg fr to peg to with help of peg h

    public static String hanoi(int n, int fr, int to, int h)
    {
        if ( n == 1 )
	{  // base case
	   return fr + " --> " + to + "\n";
	}
	else
	{
	    String helpSol1 = hanoi(n-1, fr, h, to);
	    String helpSol2 = hanoi(n-1, h, to, fr);
	    String myMove = fr + " --> " + to + "\n";

	    String mySol = helpSol1 + myMove + helpSol2;
	   
	    return mySol; 
        }
    }

The hanoi(n, fr, to, h) method   Demo program with main( )

We can invoke the Hanoi( ) method with any number of disks we like, e.g. using  4  disks: 

    public static void main(String[] args) 
    {
        String ans = hanoi( 4 , 1, 3, 2);
        System.out.println(ans);
    } 

    public static String hanoi(int n, int fr, int to, int h)
    {
        if ( n == 1 )
	{  // base case
	   return fr + " --> " + to + "\n";
	}
	else
	{
	    String helpSol1 = hanoi(n-1, fr, h, to);
	    String helpSol2 = hanoi(n-1, h, to, fr);
	    String myMove = fr + " --> " + to + "\n";

	    String mySol = helpSol1 + myMove + helpSol2;
	   
	    return mySol; 
        }
    }

DEMO: demo/07-recursion/05-hanoi/Hanoi.java