Review:    When can we use recursion ?

If we can use the solutions of the smaller problems to find Solution(n) (= solution of the original problem):

 
 

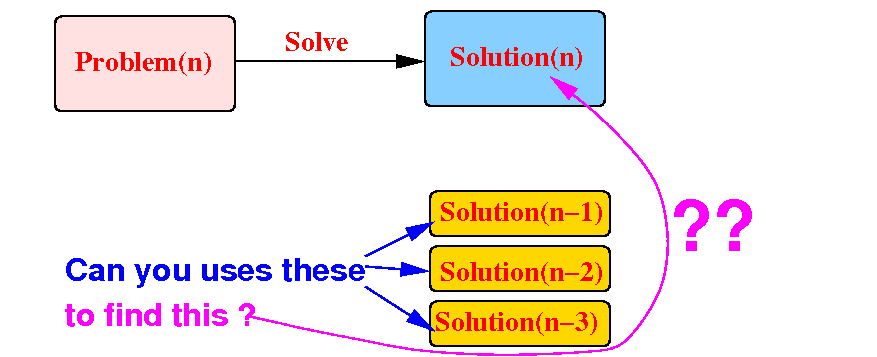
Then:   we can use recursion to solve the Problem(n)

  Palindromes  

  • Palindrome:

    • Palindrome = a string that reads the same backward as forward

    Examples: 

      mom
  radar
  racecar

  • Programming task:

    • Write a Java method that receives an input string           and

    • Returns true if the input string is a palindrome and returns false otherwise

  Can we use recursion to check for palindromes ?  

Original problem:   is some string w a palindrome ? 

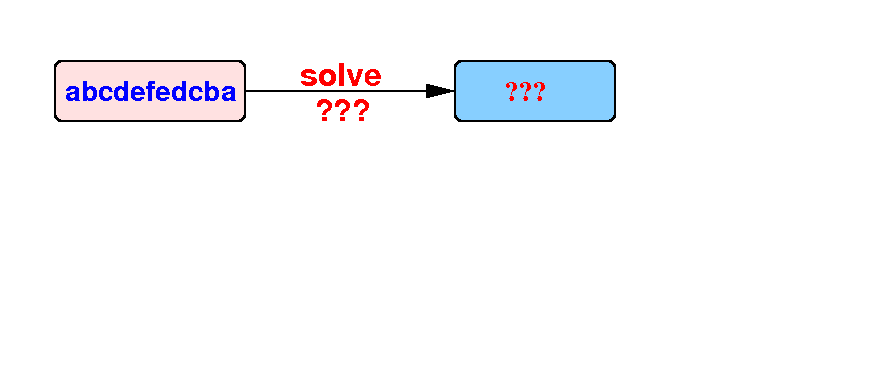
 Question: Can we use the solution of some smaller palindrome problem
           to solve this problem ???

  Can we use recursion to check for palindromes ?  

Yes, we can use the solution of this smaller problem: 

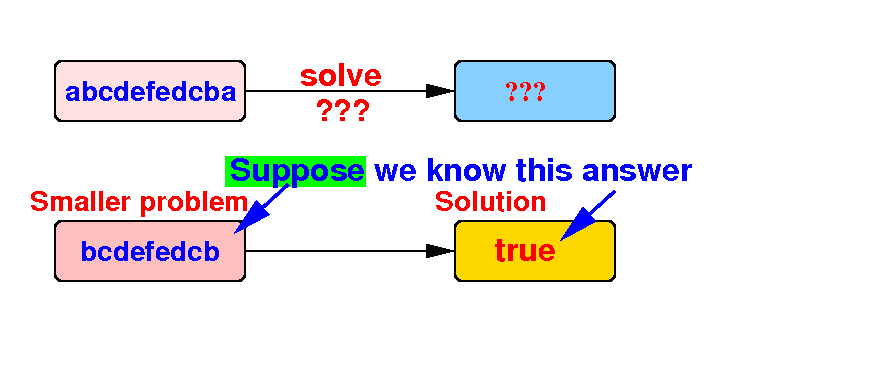
 Question:  how can we use the solution of this smaller problem 
            to solve the original problem ???

Palindrome

The string is a palindrome if (A) first char == last char and (B) smaller substring is palindrome 

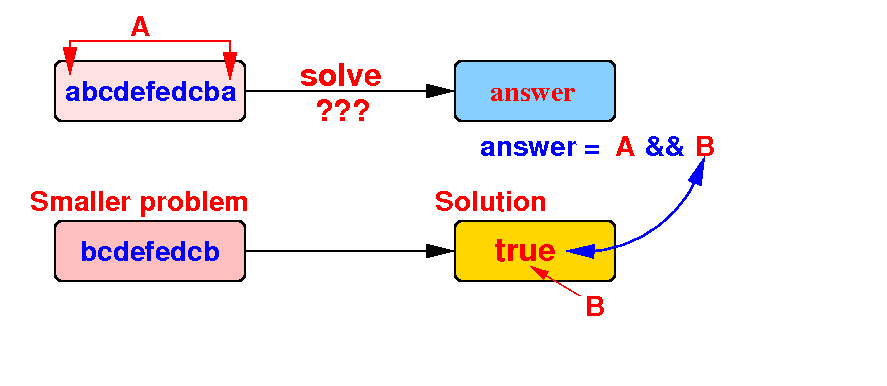
 solution(orig problem) = w.charAt(0) == w.charAt(last) && solution(smaller prob)

 Therefore, we can use recursion to solve the palindrome problem

Palindrome:   base cases

  • If you keep removing the first and last letter from a palindrome: 

         ABCDEFGHGFEDCBA
      BCDEFGHGFEDCB 
       CDEFGHGFEDC  
        DEFGHGFED   
         EFGHGFE    
          FGHGF   
           GHG    
            H  <--- easy palindrome !!

    You will end up with a string that has:

    • 0   or   1   character    ---    such a string is always a palindrome !

  • Base (= simple to solve) cases:

    • A string of length = 0 or 1 is a palindrome

Recursive isPalindrom( ) method

We now have all information needed to write the palindrome program: 

    public static boolean isPalindrome(String w)
    {
       
        

        if ( w is one of the base cases )
        {  // base cases
           return true;
        }
        else
        {
           // Use recursion to solve the original problem

           helpSol = solve the smaller problem 
           Use helpSol to solve original problem
	   Return solution
	   
        }
    }

 

Recursive isPalindrom( ) method

A word of length ≤ 1 is always a palindrome: 

    public static boolean isPalindrome(String w)
    {
        boolean helpSol;
        boolean mySol;

        if ( w.length() <= 1 )
        {  // base cases
           return true;
        }
        else
        {
           // Use recursion to solve the original problem

           helpSol = solve the smaller problem 
           Use helpSol to solve original problem
	   Return solution
	   
        }
    }

In this problem, we must solve the smaller problem by removing the first and last character

Recursive isPalindrom( ) method

Divide step:   solve this smaller problem: 

    public static boolean isPalindrome(String w)
    {
        boolean helpSol;
        boolean mySol;

        if ( w.length() <= 1 )
        {  // base cases
           return true;
        }
        else
        {
           int lastPos = w.length() - 1;
           helpSol = isPalindrome( w.substring(1, lastPos) );

	   mySol = (w.charAt(0) == w.charAt(lastPos)) && helpSol;

	   return mySol; 
        }
    }

Next, we use the solution helpSol to solve the original problem

Recursive isPalindrom( ) method

Conquer step:   solve the original problem by using helpSol: 

    public static boolean isPalindrome(String w)
    {
        boolean helpSol;
        boolean mySol;

        if ( w.length() <= 1 )
        {  // base cases
           return true;
        }
        else
        {
           int lastPos = w.length() - 1;
           helpSol = isPalindrome( w.substring(1, lastPos) );

	   mySol = (w.charAt(0) == w.charAt(lastPos)) && helpSol;

	   return mySol;
        }
    }

Final, we return the solution mySol....

Recursive isPalindrom( ) method

The isPalindrome() method written using the divide-and-conquer technique: 

    public static boolean isPalindrome(String w)
    {
        boolean helpSol;
        boolean mySol;

        if ( w.length() <= 1 )
        {  // base cases
           return true;
        }
        else
        {
           int lastPos = w.length() - 1;
           helpSol = isPalindrome( w.substring(1, lastPos) );

	   mySol = (w.charAt(0) == w.charAt(lastPos)) && helpSol;

	   return mySol;
        }
    }

DEMO: demo/07-recursion/02-palindrome/Palindrome.java

Recursive isPalindrom( ) method   simplifying the recursive code

Often, we can re-write the recursive code and make it simpler: 

    public static boolean isPalindrome(String w)
    {
        boolean helpSol;
        boolean mySol;

        if ( w.length() <= 1 )
        {  // base cases
           return true;
        }
        else
        {
           int lastPos = w.length() - 1;
           helpSol = isPalindrome( w.substring(1, lastPos) );

	   mySol = (w.charAt(0) == w.charAt(lastPos)) && helpSol;

	   return mySol;
        }
    }

(1) Replace helpSol with isPalindrome( w.substring(1, lastPos) )

Recursive isPalindrom( ) method   simplifying the recursive code

After replacing helpSol with isPalindrome( w.substring(1, lastPos) ): 

    public static boolean isPalindrome(String w)
    {
        boolean helpSol; 
        boolean mySol;

        if ( w.length() <= 1 )
        {  // base cases
           return true;
        }
        else
        {
           int lastPos = w.length() - 1;
           helpSol = isPalindrome( w.substring(1, lastPos) ); 

	   mySol = (w.charAt(0) == w.charAt(lastPos)) && 
                                   isPalindrome( w.substring(1, lastPos) );
	   return mySol;
        }
    }

(2) Return the computated result without first storing in help variable mySol...

Recursive isPalindrom( ) method   simplifying the recursive code

After "short circuiting" the computation: 

    public static boolean isPalindrome(String w)
    {
        boolean helpSol; 
        boolean mySol; 

        if ( w.length() <= 1 )
        {  // base cases
           return true;
        }
        else
        {
           int lastPos = w.length() - 1;
           helpSol = isPalindrome( w.substring(1, lastPos) ); 

	   return  (w.charAt(0) == w.charAt(lastPos)) && 
                                   isPalindrome( w.substring(1, lastPos) );
	
        }
    }

DEMO: demo/07-recursion/02-palindrome/Palindrome2.java