Factorial of
n
- In Mathematics, the
factorial of
a number
n is
defined as:
n! = n × (n−1) × (n−2) × ..... × 1
|
- Using the
same
definition, the
factorial of
a number
n−1 is
defined as:
(n−1)! = (n−1) × (n−2) × (n−3) × ..... × 1
|
-
Therefore,
we can define
n!
using
the definition of
(n−1)!
as follows:
n! = n × (n−1) × (n−2) × ..... × 1
= n × (n−1)!
|
- Example:
10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 10 × 9!
|
|
The recursive
definition
of the
facorial of
n
- The
factorial
of a number
n
(
n!)
can be recursively
defined as follows:
0! = 1 // This rule is needed to stop infinite recursion
n! = n × (n - 1)! if n > 0
|
- Example: compute 4!
4! = 4 × 3!
3! = 3 × 2!
2! = 2 × 1!
1! = 1 × 0! // stops infinite recursion
1! = 1 × 1 = 1
2! = 2 × 1 = 2
3! = 3 × 2 = 6
4! = 4 × 6 = 24
|
|
Writing a
recursive method to
compute
n!
- Let us write a
method called
factorial(n) that
computes
n!:
public static int factorial(int n)
{
// computes n!
if ( n == 0 )
return 1;
else
return n * factorial(n-1);
}
|
- The factorial method has
a
parameter variable
int n
- The factorial method
returns a
result that is an
int typed
value
|
Writing a
recursive method to
compute
n!
- If you invoke
the
factorial
method
with
n = 0,
it
returns
the result 1:
(Because:
0! = 1)
public static int factorial(int n)
{
// computes n!
if ( n == 0 )
return 1;
else
return n * factorial(n-1);
}
|
- Every
recursive method
must
solve
the simple case(s)
-
Base cases:
- The simplest cases of the
recursive problem are
called the
base cases
- The
base cases
are the
stopping conditions
for the recursion
|
|
Writing a
recursive method to
compute
n!
- If you call
the factorial method
with
n > 0, it
solves
the
n!
using the
solution of a
subproblem
that computes the
factorial of
n − 1:
public static int factorial(int n)
{
// computes n!
if ( n == 0 )
return 1;
else
return n * factorial(n-1);
}
|
-
The subproblem
of
computing
(n−1)!
is
essentially the same as the
original problem
of
computing
n!,
but it is simpler or
smaller.
-
Because
the subproblem
(n−1)!
has the
same property
as the original problem,
you can call the
factorial
method
with a
different argument(s)
- this is referred to as a
recursive call.
|
Important property of a
recursive method
- A
recursive call
can result in
many more recursive calls,
because:
- The
recursive method
divide
a subproblem
into other
even smaller
subsubproblems.
|
- For a
recursive method
to
terminate, the
problem
must
eventually be
reduced
to a
stopping case:
- A
stopping case makes a
recursive method
return
a result and
stops
"infinite" recursive
|
Example:
public static int factorial(int n)
{
// computes n!
if ( n == 0 ) <--- Stopping case
return 1;
else
return n * factorial(n-1);
}
|
|
Demonstrating the
execution of a
recursive method
I will use step into in
BlueJ to
show the execution of the
factorial( ) method:
public static void main(String[] args)
{
int r;
r = factorial(4);
}
public static int factorial(int n)
{
// computes n!
if ( n == 0 )
return 1;
else
return n * factorial(n-1);
}
|
DEMO:
demo/07-recursion/01-factorial/Factorial.java
Notice that
the activation records for
factorial(4),
factorial(3),
factorial(2),
factorial(1) and
factorial(0)
during the demo
Demonstrating the
execution of a
recursive method
The execution of
factorial(4) shows the
following
call and
return
sequence:
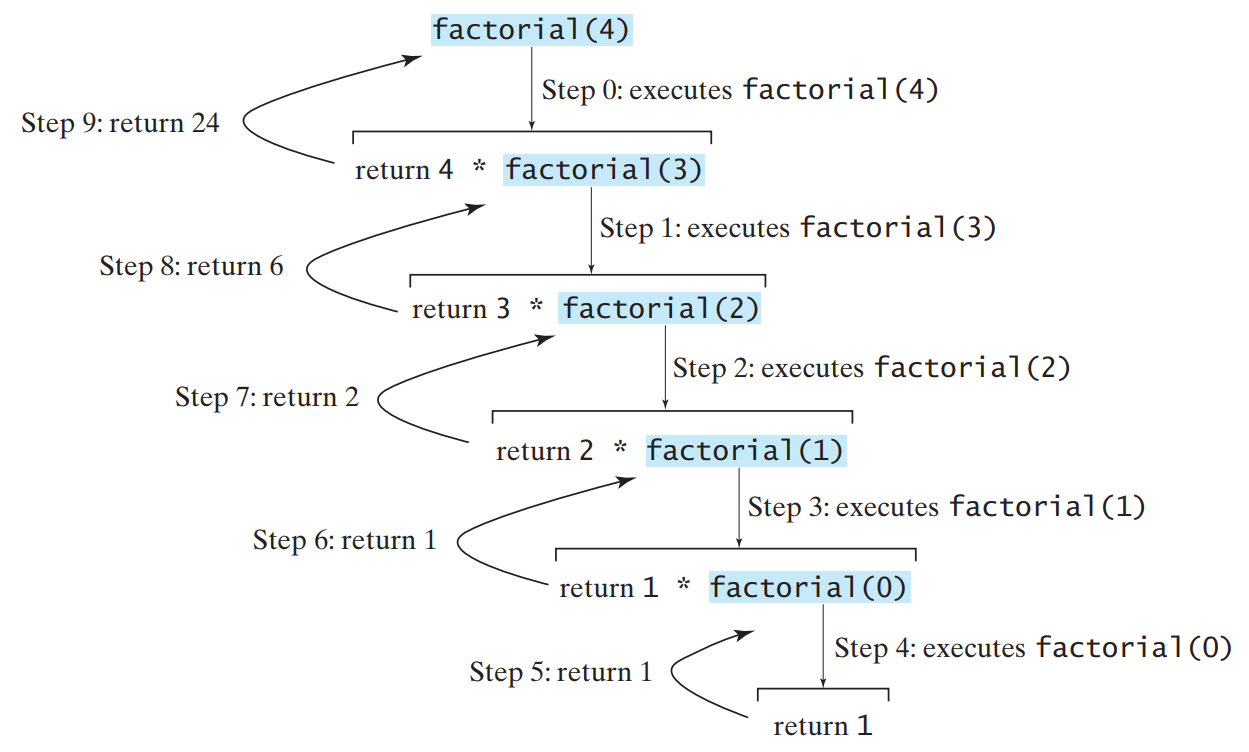
We can see that
factorial(4),
factorial(3),
factorial(2),
factorial(1) and
factorial(0) are
all active because we can
see their
activation records in
BlueJ
Infinite
recursion....
-
Infinite
recursion:
-
Infinite
recursion
is the phenomenon where
a recursion
does
not
stop
|
- If recursion
does
not
reduce to
some
base case
or a
base case
is not reached,
it will result in
infinite recursion
- Example:
public static void main(String[] args)
{
int r;
r = factorial(4);
}
public static int factorial(int n)
{
return n * factorial(n-1); // Never ending calls...
}
|
-
Infinite recursion
will cause a stack overflow
program crash
|
DEMO:
demo/07-recursion/01-factorial/InfiniteRecursion.java
❮
❯
