Searching Arrays

  • Searching:

      • Searching is a very common task in computer programming.

      • Many algorithms and data structures have been invented to support fast searching.

  • Seaching arrays:

      • Arrays are often used to store a large amount of data

      • Searching is the process of looking for a specific element in an array

      • There are 2 search algorithms designed for arrays:

        1. The linear search algorithm

        2. The binary search algorithm

The search problem for an array

  • The search problem for arrays is:

    • You are given a search value key

      Problem:

      • Find the index of the (first) array element that contains the search value key

    • Return −1 when the key is not found in the array

  • Example: 

                        0  1  2  3  4   5  6  7  <---- array index
    int[] myList = {1, 4, 4, 2, 5, -3, 6, 2};

    int i = arraySearch(myList,  4); // Returns   1
    int j = arraySearch(myList, -4); // Returns  -1
    int k = arraySearch(myList, -3); // Returns   5

The linear search algorithm for arrays

  • The linear search algorithm compares the search value key sequentially with each element in the array.

        

  • The linear search algorithm continues to do so until the key matches an element in the array or the array is exhausted without a match being found.

  • If a match is made, the linear search returns the index of the element in the array that matches the key.

  • If no match is found, the search returns -1.

  • See an animation of the linear search algorithm:

The linear search algorithm for arrays

  • The linear search algorithm compares the search value key sequentially with each element in the array.

        

  • The linear search algorithm continues to do so until the key matches an element in the array or the array is exhausted without a match being found.

  • If a match is made, the linear search returns the index of the element in the array that matches the key.

  • If no match is found, the search returns -1.

  • See an animation of the linear search algorithm:

The linear search algorithm for arrays

  • The linear search algorithm compares the search value key sequentially with each element in the array.

        

  • The linear search algorithm continues to do so until the key matches an element in the array or the array is exhausted without a match being found.

  • If a match is made, the linear search returns the index of the element in the array that matches the key.

  • If no match is found, the search returns -1.

  • See an animation of the linear search algorithm:

The linear search algorithm for arrays

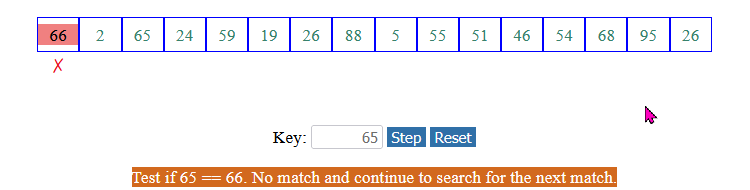
The linear search algorithm for arrays: 

    /* ----------------------------------------------------
       The linear search algorithm to find key
       in the array list
       ---------------------------------------------------- */
    public static int linearSearch(int[] list, int key)
    {
        for ( int i = 0; i < list.length; i++ )
	   if ( list[i] == key )
	       return i;

        // key was not found in list[]
	return -1;
    }

    public static void main(String[] args)
    {
        int[] myList = {1, 4, 4, 2, 5, -3, 6, 2};

	int i = linearSearch(myList,  4); // Returns  1
	int j = linearSearch(myList, -4); // Returns -1
	int k = linearSearch(myList, -3); // Returns 5
    }

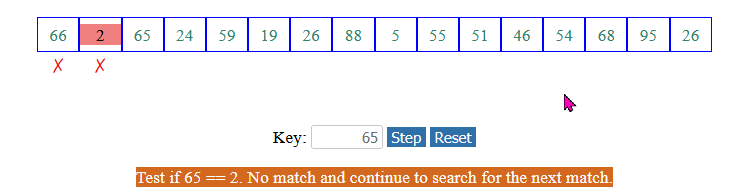
The linear search algorithm for arrays

Examine each array element sequentially: 

    /* ----------------------------------------------------
       The linear search algorithm to find key
       in the array list
       ---------------------------------------------------- */
    public static int linearSearch(int[] list, int key)
    {
        for ( int i = 0; i < list.length; i++ )
	   Does list[i] contains key ?
	       return i;

        // key was not found in list[]
	return -1;
    }

    public static void main(String[] args)
    {
        int[] myList = {1, 4, 4, 2, 5, -3, 6, 2};

	int i = linearSearch(myList,  4); // Returns  1
	int j = linearSearch(myList, -4); // Returns -1
	int k = linearSearch(myList, -3); // Returns 5
    }

The linear search algorithm for arrays

Look for the key value in each array element: 

    /* ----------------------------------------------------
       The linear search algorithm to find key
       in the array list
       ---------------------------------------------------- */
    public static int linearSearch(int[] list, int key)
    {
        for ( int i = 0; i < list.length; i++ )
	   if ( list[i] == key )
	       return i;

        // key was not found in list[]
	return -1;
    }

    public static void main(String[] args)
    {
        int[] myList = {1, 4, 4, 2, 5, -3, 6, 2};

	int i = linearSearch(myList,  4); // Returns  1
	int j = linearSearch(myList, -4); // Returns -1
	int k = linearSearch(myList, -3); // Returns 5
    }

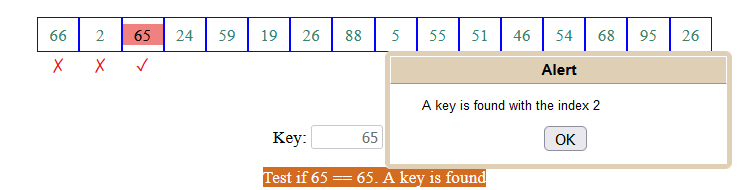
The linear search algorithm for arrays

If the key is found in list[i], we return the index i: 

    /* ----------------------------------------------------
       The linear search algorithm to find key
       in the array list
       ---------------------------------------------------- */
    public static int linearSearch(int[] list, int key)
    {
        for ( int i = 0; i < list.length; i++ )
	   if ( list[i] == key )
	       return i;

        // key was not found in list[]
	return -1;
    }

    public static void main(String[] args)
    {
        int[] myList = {1, 4, 4, 2, 5, -3, 6, 2};

	int i = linearSearch(myList,  4); // Returns  1
	int j = linearSearch(myList, -4); // Returns -1
	int k = linearSearch(myList, -3); // Returns 5
    }

The linear search algorithm for arrays

When all elements have been searched, then we know that the key is not found in the array ==> return -1. 

    /* ----------------------------------------------------
       The linear search algorithm to find key
       in the array list
       ---------------------------------------------------- */
    public static int linearSearch(int[] list, int key)
    {
        for ( int i = 0; i < list.length; i++ )
	   if ( list[i] == key )
	       return i;

        // key was not found in list[]
	return -1;
    }

    public static void main(String[] args)
    {
        int[] myList = {1, 4, 4, 2, 5, -3, 6, 2};

	int i = linearSearch(myList,  4); // Returns  1
	int j = linearSearch(myList, -4); // Returns -1
	int k = linearSearch(myList, -3); // Returns 5
    }

DEMO: demo/08-array/11-searching/LinearSearch.java

The binary search algorithm for arrays

  • Binary search is a more efficient (= faster) search algorithm for arrays.

  • Requirement to use binary search:

    • For binary search to work, the elements in the array must be ordered.

  • Assumption:

    • For the presentation of the binary search, we assume that the array is in ascending order.

  • The binary search compares the key with the element in the middle of the array: 

        if ( key == list[middle] )
        return middle;               // found !
    else if ( key < list[middle] )
        continue the search in first half of the array
    else
        continue the search in second half of the array

The binary search algorithm for arrays

  • Compare the key with the middle element in the array:

            Because 52 < 64, we continue the search in the first half of the array.

  • Notice that the middle element in the first half of the array = 42

  • See an animation of the binary search algorithm:

The binary search algorithm for arrays

  • Compare the key with the middle element in the array:

            Because 52 > 42, we continue the search in the second half of the array.

  • And so on (check out the animation)

  • See an animation of the binary search algorithm:

The binary search algorithm for arrays

The binary search algorithm for arrays starts with low and high being equal to the end points of the array: 

             +---+---+---+---+---+---+---+---+---+---+---+---+---+
    list[]:  |   |   |   |   |   |   |   |   |   |   |   |   |   |
             +---+---+---+---+---+---+---+---+---+---+---+---+---+
               ^                                               ^
	       |					       |
	      low					      high

    public static int binarySearch(int[] list, int key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while (low <= high) 
	{
	    int mid = (low + high) / 2;

	    if (key == list[mid])
	        return mid;
	    else if (key < list[mid])
	        high = mid - 1;
	    else
	       low = mid + 1;
        }

        return -1; // Not found
    }

The binary search algorithm for arrays

(1) Find the middle element 

             +---+---+---+---+---+---+---+---+---+---+---+---+---+
    list[]:  |   |   |   |   |   |   |   |   |   |   |   |   |   |
             +---+---+---+---+---+---+---+---+---+---+---+---+---+
               ^                       ^                       ^
	       |		       |		       |
	      low		      mid		      high

    public static int binarySearch(int[] list, int key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while (low <= high) 
	{
	    int mid = (low + high) / 2;

	    if (key == list[mid])
	        return mid;
	    else if (key < list[mid])
	        high = mid - 1;
	    else
	       low = mid + 1;
        }

        return -1; // Not found
    }

The binary search algorithm for arrays

(2) If   key == list[mid], we found the search value key: 

             +---+---+---+---+---+---+---+---+---+---+---+---+---+
    list[]:  |   |   |   |   |   |   |key|   |   |   |   |   |   |
             +---+---+---+---+---+---+---+---+---+---+---+---+---+
               ^                       ^                       ^
	       |		       |		       |
	      low		      mid		      high

    public static int binarySearch(int[] list, int key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while (low <= high) 
	{
	    int mid = (low + high) / 2;

	    if (key == list[mid])
	        return mid;
	    else if (list[mid] > key)
	        high = mid - 1;
	    else
	       low = mid + 1;
        }

        return -1; // Not found
    }

The binary search algorithm for arrays

(3) If   key < list[mid], we continue the search in the lower half of the array: 

             +---+---+---+---+---+---+---+---+---+---+---+---+---+
    list[]:  |   |   |   |   |   |   | < |   |   |   |   |   |   |
             +---+---+---+---+---+---+---+---+---+---+---+---+---+
               ^                   ^   ^                        
	       |		   |   |		        
	      low <- new range-> high mid		      high

    public static int binarySearch(int[] list, int key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while (low <= high) 
	{
	    int mid = (low + high) / 2;

	    if (key == list[mid])
	        return mid;
	    else if (key < list[mid])
	        high = mid - 1;   // The range of the search is low - high
	    else
	       low = mid + 1;
        }

        return -1; // Not found
    }

The binary search algorithm for arrays

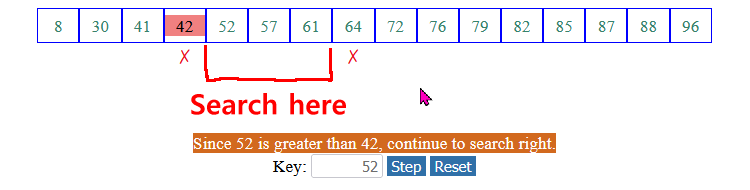
(4) Otherwise   ( key > list[mid]), we continue the search in the upper half of the array: 

             +---+---+---+---+---+---+---+---+---+---+---+---+---+
    list[]:  |   |   |   |   |   |   | > |   |   |   |   |   |   |
             +---+---+---+---+---+---+---+---+---+---+---+---+---+
                                       ^   ^                   ^
	        		       |   |		       |
	      low		      mid low <-- new range--> high

    public static int binarySearch(int[] list, int key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while (low <= high) 
	{
	    int mid = (low + high) / 2;

	    if (key == list[mid])
	        return mid;
	    else if (k < list[mid])
	        high = mid - 1;
	    else
	        low = mid + 1;    // The range of the search is low - high
        }

        return -1; // Not found
    }

The binary search algorithm for arrays

(5) We must repeat the steps for the remaining array elements:    When do we stop ? 

             +---+---+---+---+---+---+---+---+---+---+---+---+---+
    list[]:  |   |   |   |   |   |   |   |   |   |   |   |   |   |
             +---+---+---+---+---+---+---+---+---+---+---+---+---+
                                           ^                   ^
	        		           |		       |
	         		          low		      high

    public static int binarySearch(int[] list, int key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while ( low <= high ) 
	{
	    int mid = (low + high) / 2;

	    if (key == list[mid])
	        return mid;
	    else if (k < list[mid])
	        high = mid - 1;
	    else
	        low = mid + 1;
        }

        return -1; // Not found
    }

The binary search algorithm for arrays

(6) We stop when low > high.    In other words: we continue as long as low <= high: 

             +---+---+---+---+---+---+---+---+---+---+---+---+---+
    list[]:  |   |   |   |   |   |   |   |   |   |   |   |   |   |
             +---+---+---+---+---+---+---+---+---+---+---+---+---+
                                       ^   ^                    
	        		       |   |	<--- empty array
	         		     high low		          

    public static int binarySearch(int[] list, int key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while ( low <= high ) 
	{
	    int mid = (low + high) / 2;

	    if (key == list[mid])
	        return mid;
	    else if (key < list[mid])
	        high = mid - 1;
	    else
	        low = mid + 1;
        }

        return -1; // Not found
    }

The binary search algorithm for arrays

(7) we return -1 when key is not found: 

             +---+---+---+---+---+---+---+---+---+---+---+---+---+
    list[]:  |   |   |   |   |   |   |   |   |   |   |   |   |   |
             +---+---+---+---+---+---+---+---+---+---+---+---+---+
                                       ^   ^                    
	        		       |   |	<--- empty array
	         		     high low		          

    public static int binarySearch(int[] list, int key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while ( low <= high ) 
	{
	    int mid = (low + high) / 2;

	    if (key == list[mid])
	        return mid;
	    else if (key < list[mid])
	        high = mid - 1;
	    else
	        low = mid + 1;
        }

        return -1; // Not found
    }

The binary search algorithm for arrays   Demo program 

    public static void main(String[] args)
    {
        int[] myList = {1, 5, 9, 17, 19, 78, 99, 143, 450, 876, 999};
        int r;
        
        r = binarySearch(myList, 143);
        System.out.println("r = " + r);
    }

    public static int binarySearch(int[] list, int key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while ( low <= high ) 
	{
	    int mid = (low + high) / 2;

	    if (key == list[mid])
	        return mid;
	    else if (key < list[mid])
	        high = mid - 1;
	    else
	        low = mid + 1;
        }

        return -1; // Not found
    }

DEMO: demo/08-array/11-searching/BinarySearch.java

The binary search algorithm for arrays of strings

The binary search algorithm can be adapted to work with arrays of Strings as follows: 

                                 String[]    String
    public static int binarySearch(int[] list, int key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while ( low <= high ) 
	{
	    int mid = (low + high) / 2;

	    if (key == list[mid])     // How to test if string1 == string2?
	        return mid;
	    else if (key < list[mid]) // How to test if string1 > string2?
	        high = mid - 1;
	    else
	        low = mid + 1;
        }

        return -1; // Not found
    }

Hint: let the Java compiler help you find the necessary changes in the program !

The binary search algorithm for arrays of strings

The binary search algorithm for String must use compareTo( ) to compare String values: 

 
    public static int binarySearch(String[] list, String key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while ( low <= high ) 
	{
	    int mid = (low + high) / 2;

	    if (key.compareTo(list[mid]) == 0)  
	        return mid;
	    else if (key.compareTo(list[mid]) < 0)
	        high = mid - 1;
	    else
	        low = mid + 1;
        }

        return -1; // Not found
    }

Next slide has the demo program....

The binary search algorithm for arrays of strings   -   demo program 

    public static void main(String[] args)
    {
        String[] myList = {"abe", "becky", "clair", "henry", "norm", "sam"};
        int r;
        
        r = binarySearch(myList, "sam");
        System.out.println("r = " + r);
    }

    public static int binarySearch(String[] list, String key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while ( low <= high ) 
	{
	    int mid = (low + high) / 2;

	    if (key.compareTo(list[mid]) == 0)  
	        return mid;
	    else if (key.compareTo(list[mid]) < 0)
	        high = mid - 1;
	    else
	        low = mid + 1;
        }

        return -1; // Not found
    }

DEMO: demo/08-array/11-searching/StringBinarySearch.java