The union-find algorithm supports 2 operations:

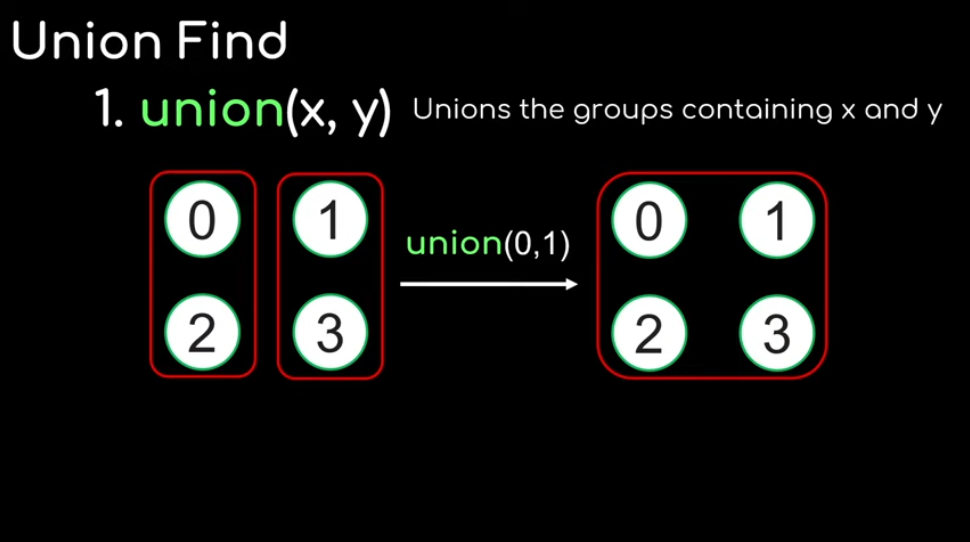
 (1) union(x,y)  unions the groups containing x and y into 1 group
  

The union-find algorithm supports 2 operations:

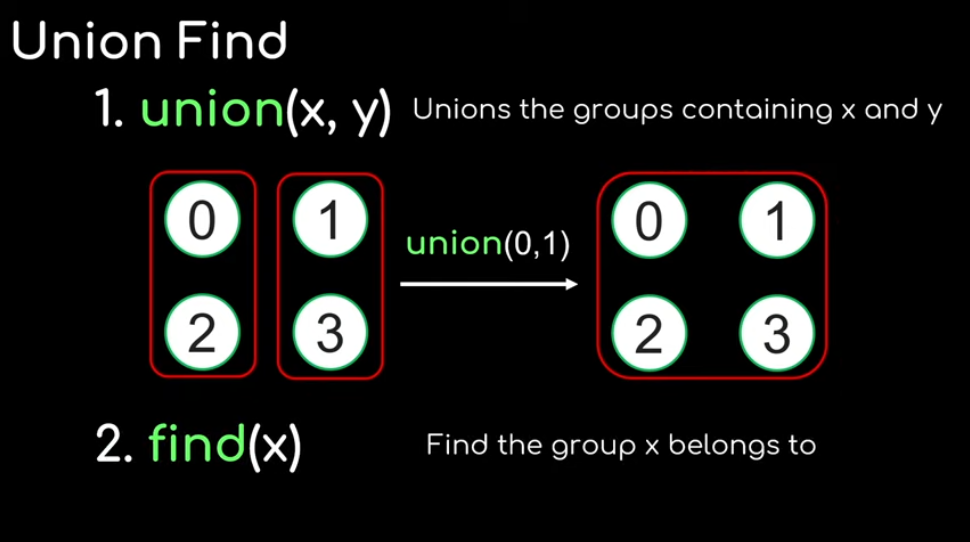
 (2) find(x)  finds the group containing x 

Suppose we have these groups:

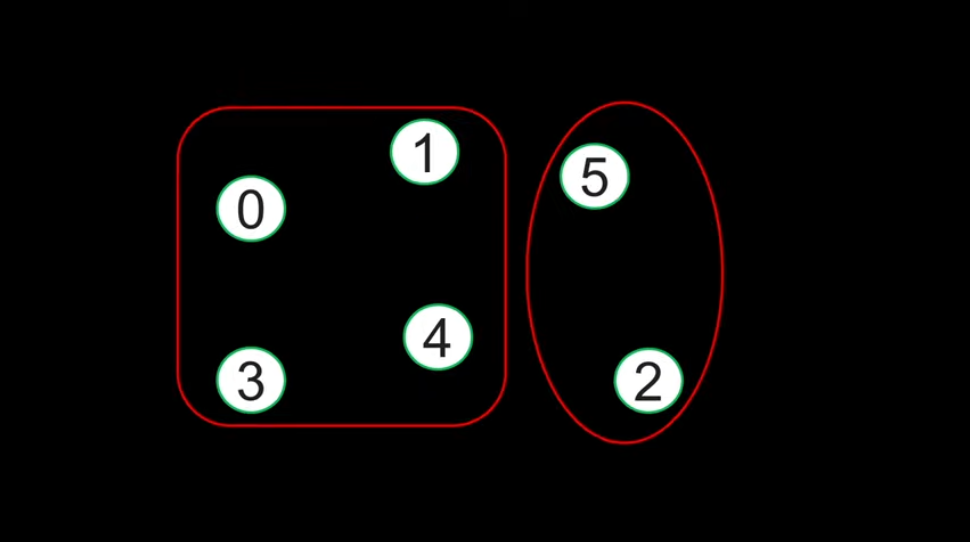
  Group 1:  0, 1, 3, 4
  Group 2:  2, 5 

How these groups are represented:

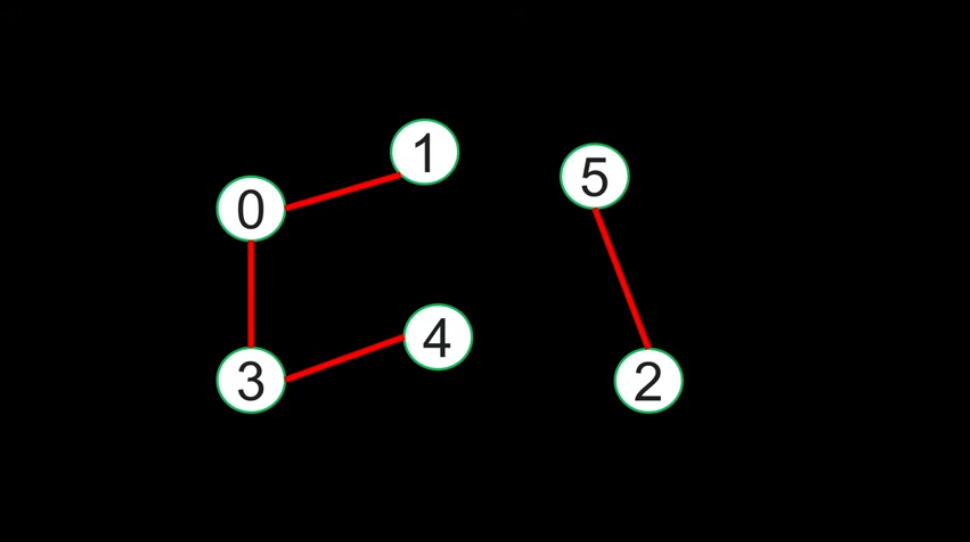
   Nodes in same group are connected with edges into a tree
  

How these groups are represented:

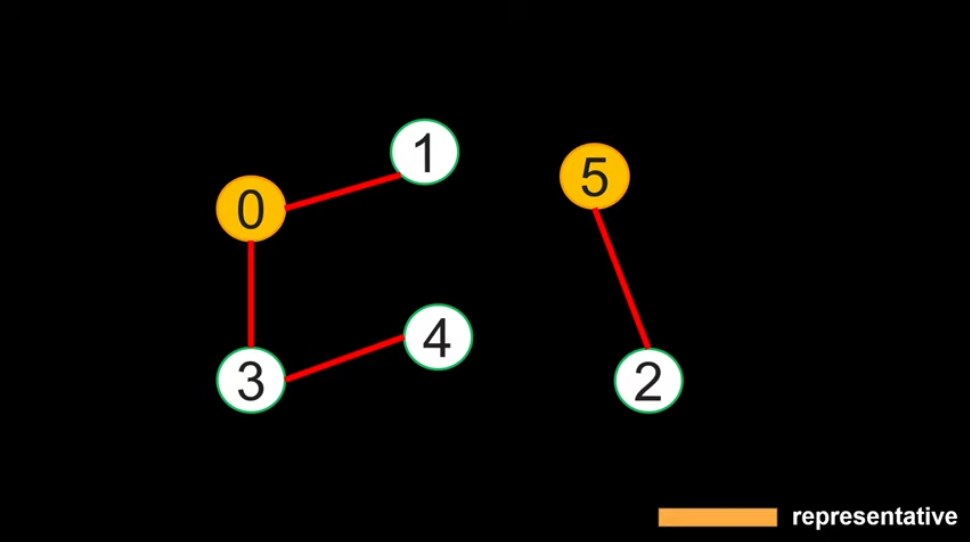
   The root node of a tree is the "representative" element 
   of the (entire) group 

How these groups are represented:   (actual representation)

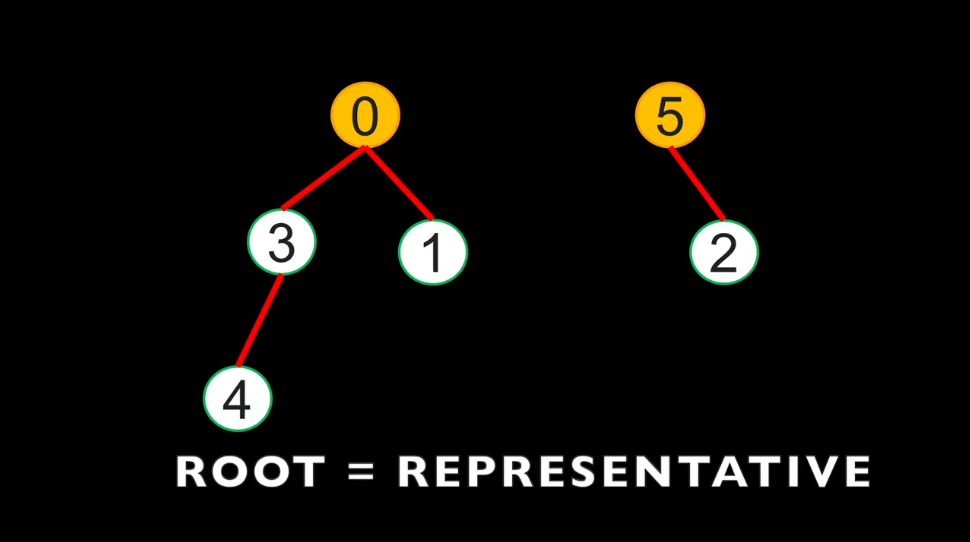
   The root node of a tree is the "representative" element 
   of the (entire) group 

The Find(x) function:

   The find(x) function will return the "representative" node
   of the group that contains x 

The Find(x) function:

   The find(x) function will return the "representative" node
   of the group that contains x 

The Find(x) function:

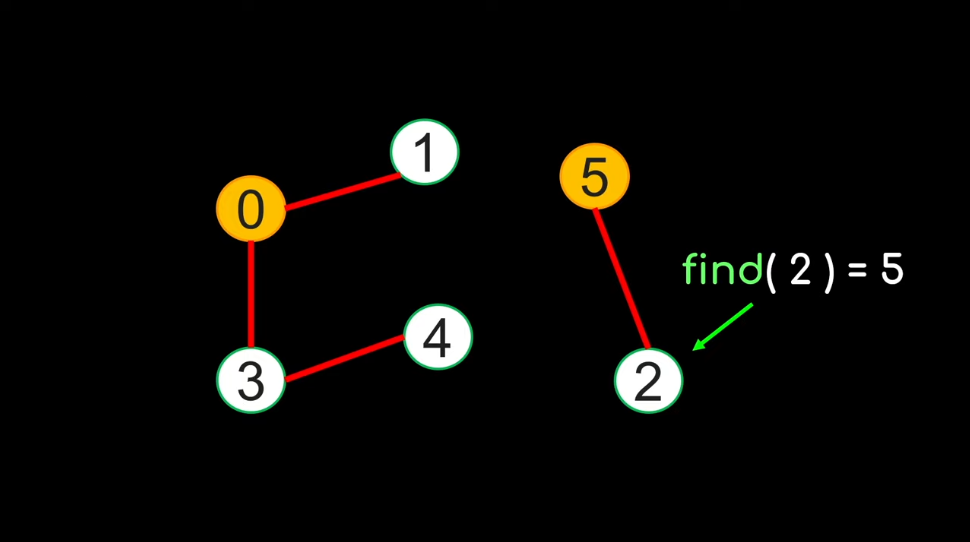
   The find(x) function will return the "representative" node
   of the group that contains x 

Question:   How can we tell if 2 elements x and y belongs to the same group ?

Question:   How can we tell if 2 elements x and y belongs to the same group ?

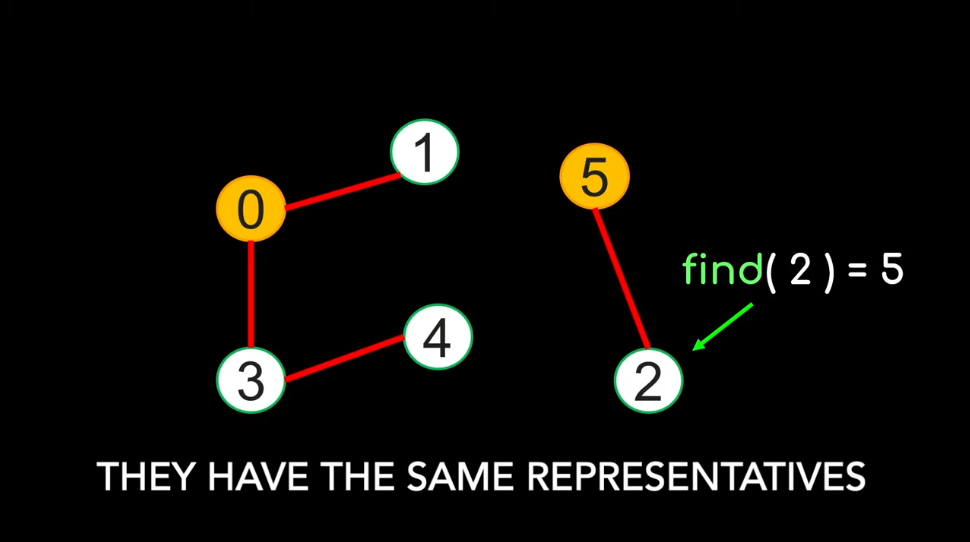
   x and y belong to same group   <===>  Find(x) == Find(y)
 

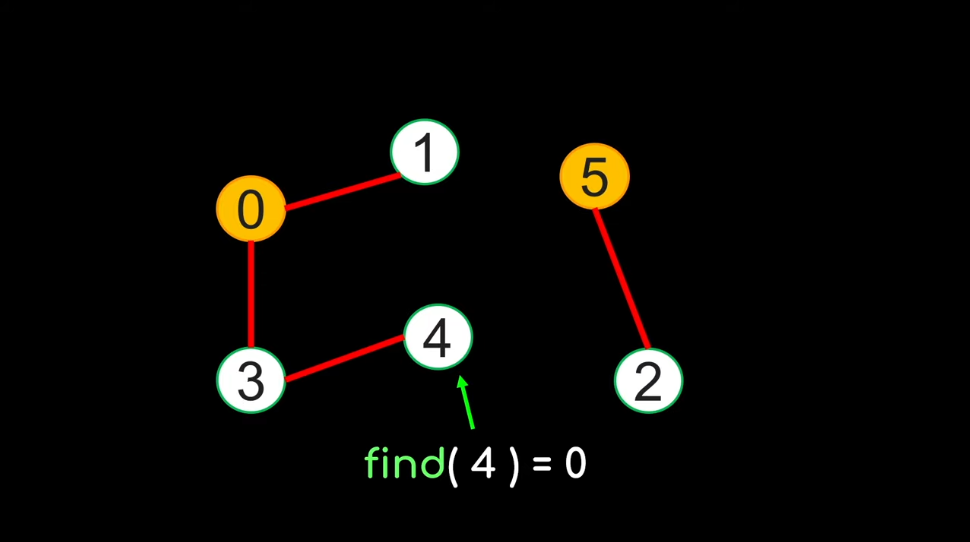
Implementing the Find(x) function:

   Find(4) = ??
 

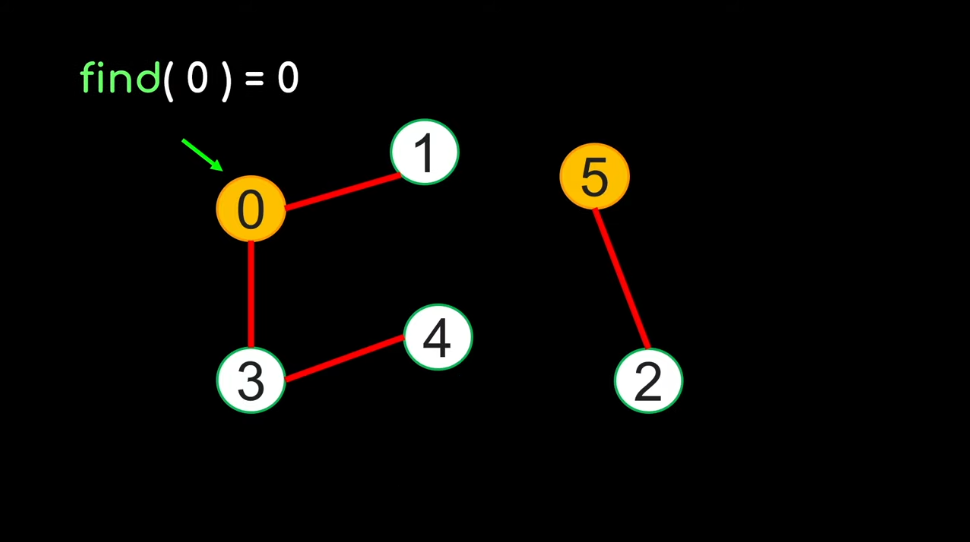
Implementing the Find(x) function:

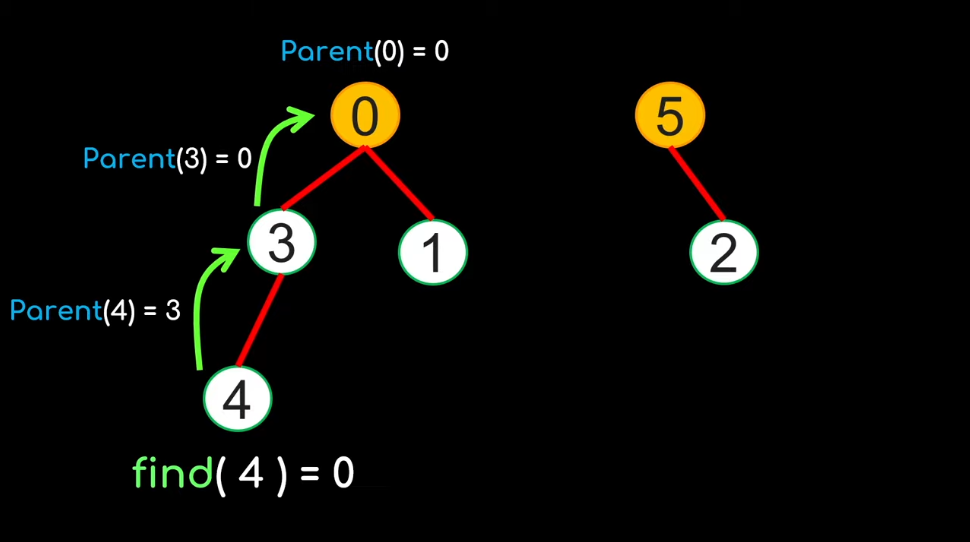
   Find(4) = 0
   Follow the parent link until you find the root node

Important take-away from the implementation of the Find(x) function:

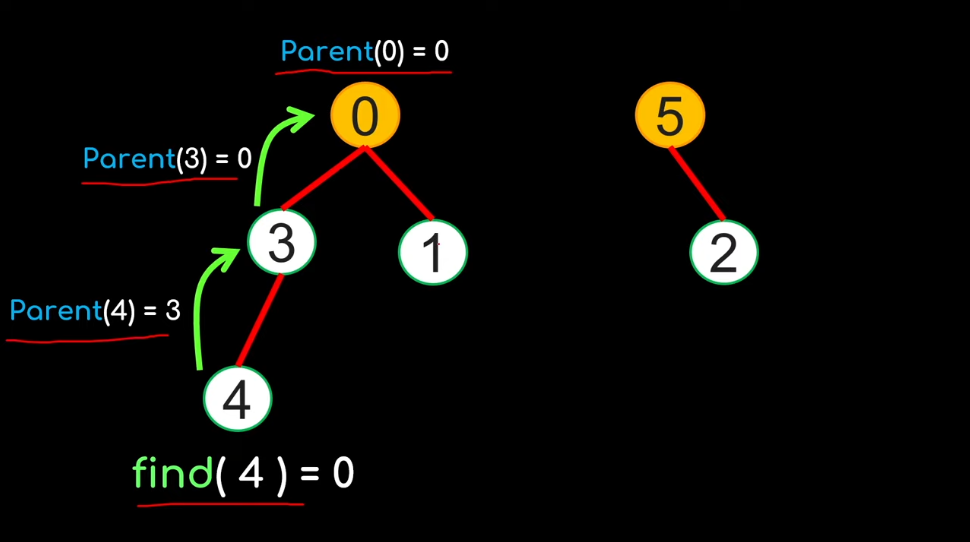
   We only need the parent link (no child links necessary)

Implementing the Union(x, y) function:

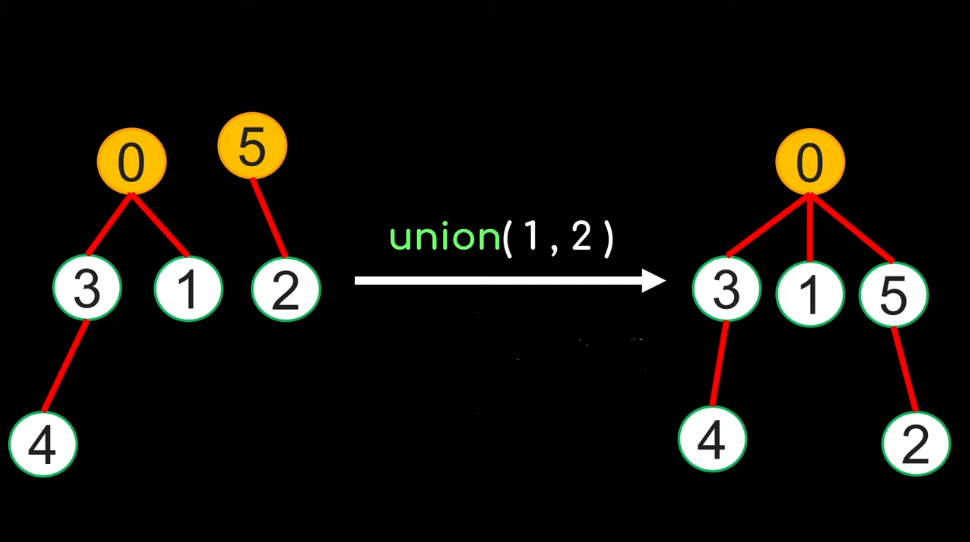
   Union(1, 2) ==> Make group(2) into a subtree of root of group(1)
 

Implementing the Union(x, y) function:

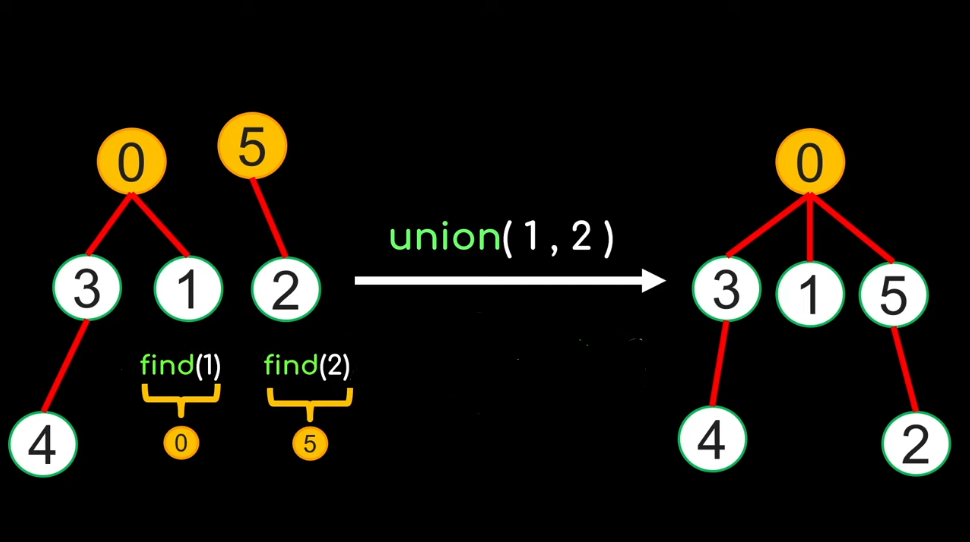
   (1) Find root(1) = Find(1) and root(2) = Find(2)
 

Implementing the Union(x, y) function:

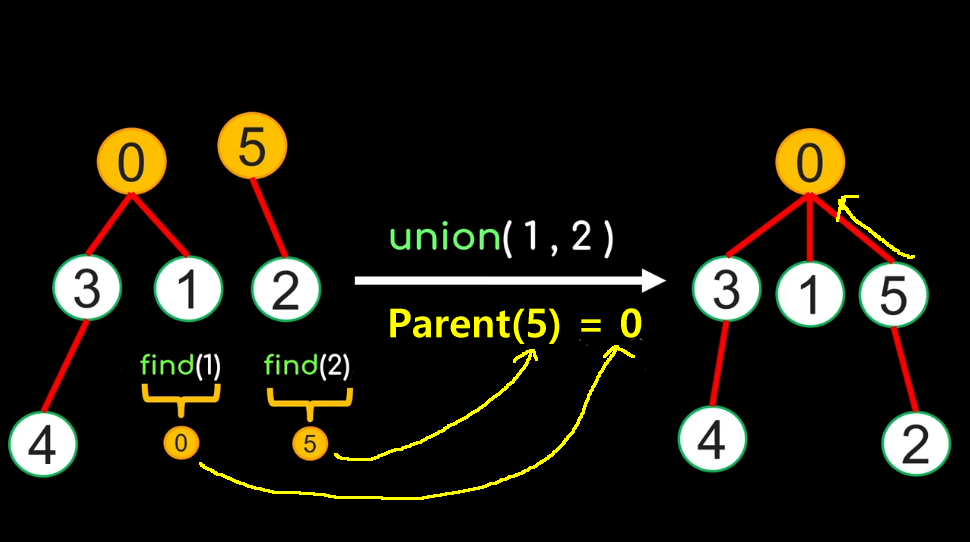
   (2) Set:  parent(root(2)) = root(1) 
 

To represent the tree, we only need the parent link:

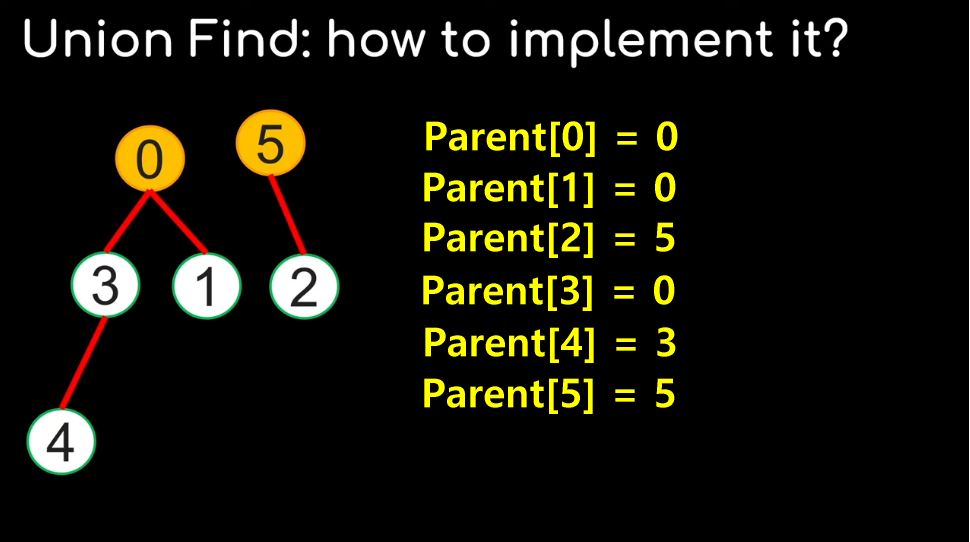
   Parent[i] = node ID of the parent node of i
   Initially:  every node forms its own group

Initial state:

   Initially:  every node forms its own group

Find(x):   traverse the parent link until you reach the root node:

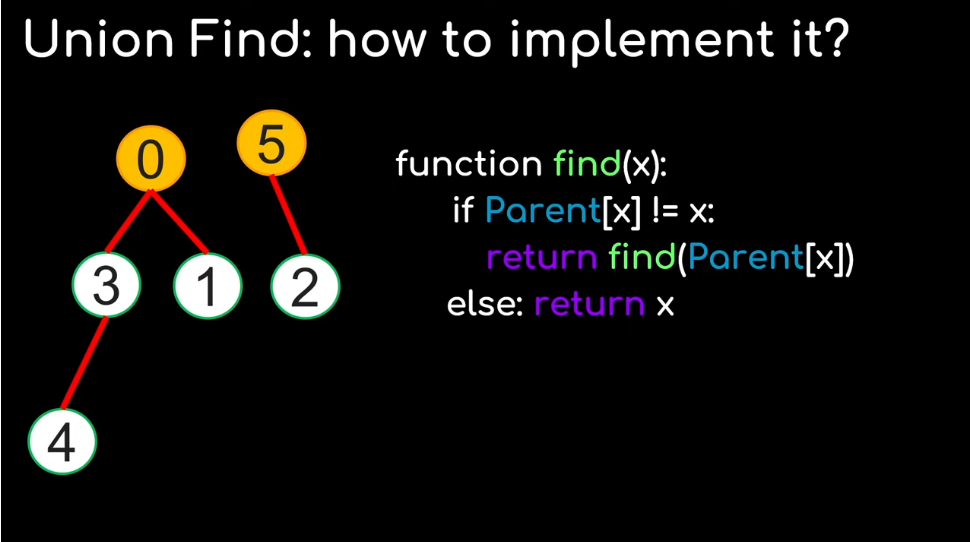
   The root node is a node x where Parent[x] == x

Union(x, y):   sets the parent node ID of root(y) (= Find(y)) to the node root(x) (= Find(x)):

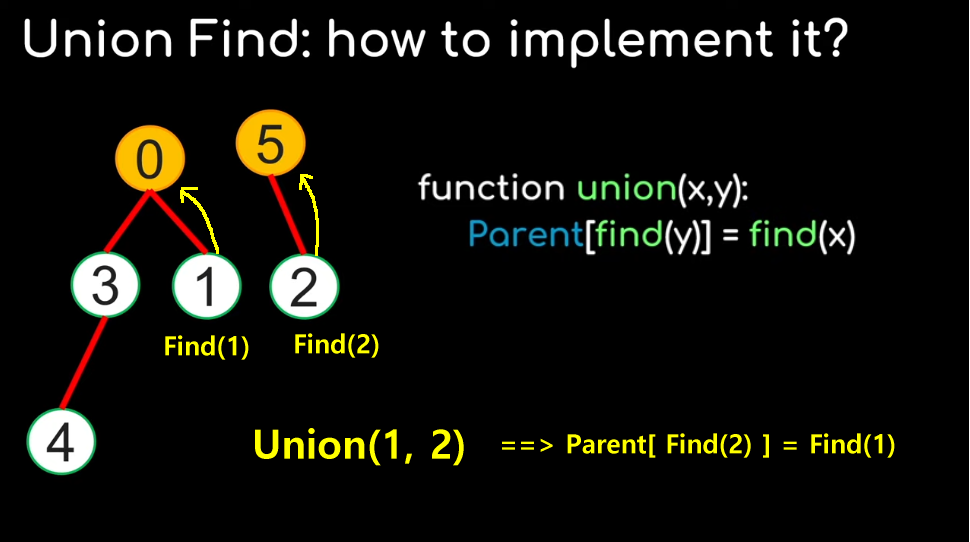
   This concludes the discussion on the Union-Find algorithm